Maclaurin Series Log1+x

Solved In 1x Can Be Approximated Using The Following Mac Chegg Com

Chapter Vi
Expand Log 1 Sinx Up To The Term Containing X 4 By Using Maclaurin S Theorem Sarthaks Econnect Largest Online Education Community

Taylor Series Wikipedia

Taylor Series Wikipedia

Taylor Series Wikipedia
Find the Maclaurin series expansion for f = sin(x)/x.

Maclaurin series log1+x. We use the trigonometric identity \({\cos ^2}x \) \(= {\large\frac{{1 + \cos 2x}}{2}\normalsize}.\) As the Maclaurin series for \(\cos x\) is \(\sum\limits. It is in fact (and please don't ask me why) correct up a few terms if you finish what you tried. Also, register with BYJU'S to get more Maths-related formulas with a detailed explanation.
In Mathematics, the Taylor series is the most famous series that is utilized in several mathematical as well as practical problems. Therefore, this is our. Taylor series approximation of this expression does not have a fifth-degree term, so taylor approximates this expression with the fourth-degree polynomial:.
You will have to figure out how many terms of the series must be used. Let f(x)=log(1+x) The Maclaurin expansion is f(x)=f(0) +xf'(0)+ (x²/2!)f''(0)+…. Get the free "Log(1-x) Taylor Series" widget for your website, blog, Wordpress, Blogger, or iGoogle.
For each of the following functions, find the Maclaurin series and its interval of convergence. In case you don’t know what f (n) (0) means, it is the n th derivative of f(x) evaluated at 0.For example, f (4) (0) is the fourth derivative of f(x) with x = 0. As x moves away from 0, you need to calculate more terms to get the same level of precision.
Find the first three nonzero terms of the Maclaurin series expansion of the given function. Determine whether the infinite series, sigma(((-1)^(n+1))/n)^2 converges or diverges. In order to get the Maclaurin series for s i n h − 1 x , we can integrate this obtained series.
So let's remind ourselves what a Maclaurin polynomial is, a Maclaurin polynomial is just a Taylor polynomial centered at zero, so the form of this second degree Maclaurin polynomial, and we just have to find this Maclaurin expansion until our second degree term, it's going. Calculus - Alternating Series Test. This exercise nails e 0 exactly, and approximates e 1 to two decimal places.
3 x fx x In part (a) students were asked for the first four nonzero terms and the general term of the Maclaurin series for f. The natural logarithm of a number is its logarithm to the base of the mathematical constant e, where e is an irrational and transcendental number approximately equal to 2.718 281 8 459.The natural logarithm of x is generally written as ln x, log e x, or sometimes, if the base e is implicit, simply log x. However, this is only the maclaurin series for the derivative of s i n h − 1 x .
Use the Maclaurin Series to find a series for. A-Evaluate the integral from 0 to 1/2 of ln(1+x)dx with an accuracy of 10^-4 using techniques of integration and a calculator. = x − 6 x 3 + 4 0 3 x 5 − 1 1 2 5 x 7 +.
Log = 2x. The standard definition of an algebraic function is provided using an algebraic equation. Differentiating it again simply increases the power as you can see.
My professor gave these in a problem set after he taught the alternating series test. The interval of convergence is (1, 1). By integrating the above Maclaurin series we find the Maclaurin series for log(1 − x), where log denotes the natural logarithm:.
Taylor polynomials can be used to approximate a function around any value for a differentiable function.In other words, when you use a Taylor series, you assume that you can find derivatives for your function. Find the Maclaurin series for f(x). Show that, \log (1+x)=x-\frac {x^2} {2}+\frac {x^3} {3}+\cdots.
F (n)(x)=ex for all n f (n)(0) = 1 for all n. Once you differentiate, you end up with a simple reciprocal. But now, you can begin to see why.
Anyway, this is not the standard way of finding a MacLaurin Series of a given function. However, the Maclaurin series for e x works best when x is close to 0. ( 1 + x) = 0 + x ( 1) + x 2 2!.
Calculadora gratuita de séries de Taylor-Maclaurin - Encontrar a representação em séries de Taylor/Maclaurin de funções passo a passo. Since sin 0 = 0, it is the cosine derivatives, which will yield a result. And the corresponding Taylor series for log(x) at a = 1 is and more generally, the corresponding Taylor series for log(x) at some is:.
( – 6) + ⋯ ln. B- Now approximate the integral from 0 to 1/2 of ln(1+x)dx to an accuracy of 10^-4 using the Maclaurin series of ln(1+x) and term-by-term integration. Which is the Binomial series.
Find the Maclaurin expansion of. The default truncation order is 6. The Taylor theorem expresses a function in the form of the sum of infinite terms.
And like always, pause this video and see if you could have a go at it. If you want to use the long method, remember that a Maclaurin series for a function is given by. You won’t use an infinite series to calculate the approximation.
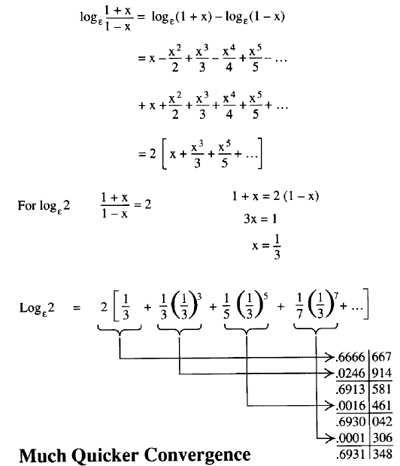
Question 7 Not yet answered Q292 Consider the Maclaurin series for 2 H log((1+x)/(1 – x)) and 2 Het:. Using this general formula, derive the Maclaurin expansion of sin 2x. Ln(1+x/1-x) = ln(1 + x) - ln(1-x) = x - x^2/2 + x^3/3-x^4/4…… - ( - x - x^2/2 - x^3/3-x^4/4…… ) = 2(x + x^3/3 + x^5/5……).
\displaystyle \begin {align*} f (x) = \sum_ {n = 0}^ {\infty} \frac {f^ { (n)} (0)} {n!}x^n \end {align*} So evaluating the derivatives gives. Find the Maclaurin expansion of. Outside the domain, the Maclaurin series either is undefined or does not relate to the function.
I was tasked to find the Maclaurin Series Representation of ln(1-x) but I'm not sure if both are the same thing and yield same answers or if the Maclaurin rep has additional steps. Maclaurin series is just a Taylor series expanded at x = 0. ( 2) + x 4 4!.
\(p_0(x)=1;p_1(x)=1−x;p_2(x)=1−x+x^2;p_3(x)=1−x+x^2−x^3;p_n(x)=1−x+x^2−x^3+⋯+(−1)^nx^n=_{k=0}^n(−1)^kx^k\) Taylor’s Theorem with Remainder Recall that the n th Taylor polynomial for a function \(f\) at a is the nth partial sum of the Taylor series for \(f\) at a. The Maclaurin series for 1 / 1 − x is the geometric series + + + + ⋯, so the Taylor series for 1 / x at a = 1 is. It depends on the centre, for some centres it is infinity and for others it is zero (divergent) (applies to both series) For S.
In the next example, we find the Maclaurin series for e x and and show that these series converge to the corresponding functions for all real numbers by proving that the remainders for all real numbers x. F(x) = 1/(1-x) It seems to me that the easiest way to find the Maclaurin Series is basically to start to write down the multiplier for (1-x) that results in a value of 1. The general formula for a Maclaurin series is:.
It really helps us a lot. The sequence of steps is very similar to the sin x derivation that was shown earlier. Maclaurin Series of ln (1+x) ( 1 + x) by using Maclaurin’s series expansion function.
As you can see ln1 = 0. The Maclaurin series generates good approximations of f(x), as long as x is close to 0. Consider the function of the form \f\left( x \right) = \sqrt {1 + x} \.
F(x) = ln(1 - x^2). We start by working out a taylor series for ln(1 +x). ( – 1) + x 3 3!.
F(0)=log(1+0)=log(1)=0 f'(x)=Dlog(1+x) f'(x)=1/(1+x) f'(0)=1/(1+0)=1 f''(x)=-1. F (x) = ∞ ∑ n=0 f n(0) n!. (1+x) log = 2x - * + 2 -X-1 = Si = 1 + 2x + 3x?.
$\textbf {\begin {pmatrix}\square&\square\\ \square&\square\end {pmatrix}}$. Use the Maclaurin Series to find a series for. Answer to m=0 n!.
Get the Maclaurin Series formula with solved examples at BYJU'S. The default truncation order is 6. I will be expanding around 0, so it will be a Maclaurin series.
The Maclaurin Series for the function 1/(1-x) is constructed in this video. By signing up, you'll get thousands of step-by-step solutions to your homework questions. Parentheses are sometimes added for clarity, giving ln(x), log e (x), or log(x).
If you liked what you read, please click on the Share button. The help is much appreciated. 9 x 4 − 6!.
(1 < x < 1) Since this power series represents ex with radius of convergence R = 1, it must be the Taylor series (about 0). The Maclaurin series for e x allows you to calculate this function for any value of x to any number of decimal places. The radius of convergence is half the length of the interval;.
Maclaurin Series for ln (1+x) Deriving the Maclaurin expansion series for ln (1+x) is very easy, as you just need to find the derivatives and plug them into the general formula. You can find actual radius of convergence with ratio test. In this tutorial we shall derive the series expansion of $$\sqrt {1 + x} $$ by using Maclaurin's series expansion function.
100 Consider the Maclaurin series for x log((1 + x)/(1 - x)) and X - 1/1 - x)":. Find the Maclaurin series for 1 / 1 + x. Find the first three nonzero terms of.
Infinity to infinity and the Siri's generated by, um, the natural log of one plus X is sigma for men equals one to infinity Negative once a part of n minus one. The Taylor series for the exponential function ex at a = 0 is. By Taylor's Theorem we know that the series expansion is then given by.
The problem here is that Taylor series doesn't converge for any number larger than 2, in other words Taylor series for ln(1+x) doesn't converge for x > 1. For ln(1+x), try the following. For ln(x) the series does not exist.
By using this website, you agree to our Cookie Policy. 1/(1-x) = sum_(k=0)^oo x^k Given:. Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on YouTube.
When -x is multiplied by 1 it. This converges are negative. Recall, a MacLaurin Series Expansion is a Taylor Series Expansion centered at $0$.
Free math lessons and math homework help from basic math to algebra, geometry and beyond. These terms are determined from the derivative of a given function for a particular point. Taylor polynomials look a little ugly, but if you break them down into small steps, it.
Konstantin Lakic Wendi Ma. Find more Mathematics widgets in Wolfram|Alpha. When a = 0, the series is also called a Maclaurin series.
The Maclaurin's series for ln(1+x) could be used to approximate the natural logarithm ln(x). The interval of convergence is the open, closed, or semiclosed range of values of x x x for which the Maclaurin series converges to the value of the function;. = 1 − 2 1 x 2 + 4!.
Taylor series expansions of logarithmic functions and the combinations of logarithmic functions and trigonometric, inverse trigonometric, hyperbolic, and inverse hyperbolic functions. X n = X1. The Taylor series for any polynomial is the polynomial itself.
In this problem the first four nonzero terms and the general term of the Maclaurin series for ln 1 x are given, and the function f is defined by ln 1. 2 2 5 x 6 +. Though, the computation of an infinite sum which give the value of a function in terms of the derivatives evaluated at a special case where x0 = 0,in contrast with Taylor series.
Find the first five terms of a power. $\textbf {\overline {x}\space\mathbb {C}\forall}$. Students, teachers, parents, and everyone can find solutions to their math problems instantly.
Free Maclaurin Series calculator - Find the Maclaurin series representation of functions step-by-step This website uses cookies to ensure you get the best experience. By signing up, you'll get thousands of step-by-step solutions to your homework. This means we need to work out the nth derivative of ln(1 + x).
It is also the radius of the circle in the complex plane within which the. Use multiplication of power series to find the first three non-zero terms of the Maclaurin series of e^x ln(1 − x). We substitute the values into the general formula to find the expansion series of sin 2x.
(CALCULUS) Power Series Representation VS. The first term of the multiplier will be 1, in order to get 1 when multiplied, so add that to the right hand side:. Alternatively, we can compute the Maclaurin series from definition.
F(x) = sinx. + X+1 = S2 What is the radius of convergence of each of these series around their centre?.

Chapter Vi
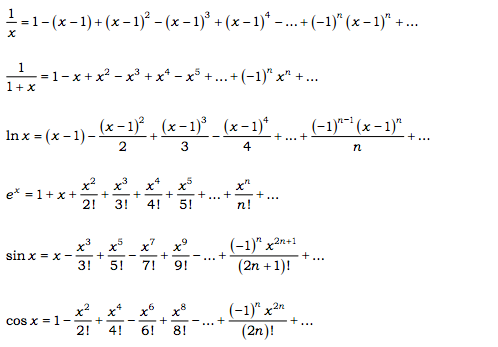
Cochranmath Taylor Series Integration And Differentiation
Taylor Series

Taylor Series

Power Series Taylor S And Maclaurin S Series

In Maclaurin Series Of Sin2x The Coefficient Of The Third Term Is

Solved Derive The Tylor Series Expansion For Log 1 X Chegg Com
Q Tbn 3aand9gctlcjugshanpv Xexyyrw4nyaxmkw0djgyjfessp7xhb6sqgy1x Usqp Cau

Natural Logarithm Wikipedia

Power Series Taylor S And Maclaurin S Series
Expand Log X In Powers Of X 1 By Taylor S Series Sarthaks Econnect Largest Online Education Community

Java Math Exercises Calculate E Raise To The Power X Using Sum Of First N Terms Of Taylor Series W3resource

Solved The Maclaurin Series Expansion For The Natural Log Chegg Com

Taylor Series For Ln 1 X How To Steps Video Lesson Transcript Study Com

Cochranmath Taylor Series Of A Function By Equating Derivatives

Solved In 1 X Can Be Approximated Using The Following Chegg Com

Serie De Maclaurin Ln 1 X Youtube
Edumatth Weebly Com Uploads 1 3 1 9 Taylor Series Pdf
Q Tbn 3aand9gctsgw9vft4mnh Bijnjv0lau9ncbgfjor ujy9dpdwsb5rxwi Usqp Cau

Taylor Series

Taylor Series Numerical Methods Projects

Solved Matlab Problem A Taylor Series Expansion About 0 Chegg Com

Worked Example Recognizing Function From Taylor Series Video Khan Academy

How Do You Find The Maclaurin Series For F X Ln Cosx Socratic

Taylor Series Wikipedia
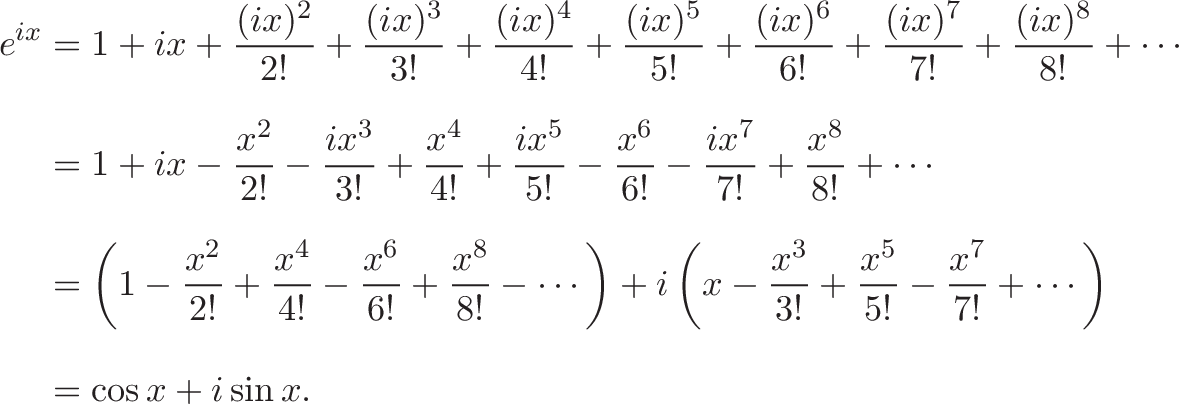
Intuition For Taylor Series Dna Analogy Betterexplained
3
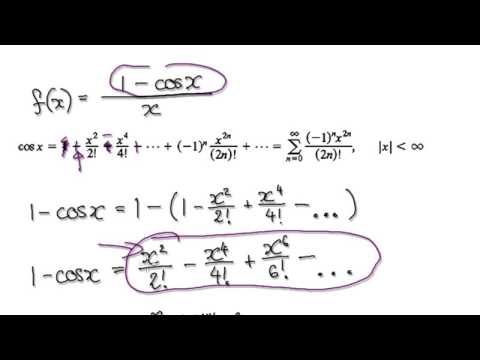
Video 2776 Maclaurin Series 1 Cosx X Practice Youtube

9 Maclaurin S Theorem Problem 1 Differential Calculus Youtube

Taylor Series For Ln 1 X How To Steps Video Lesson Transcript Study Com
Expand 1 Dim Vector By Using Taylor Series Of Log 1 E X In Python Stack Overflow
Expand E X Log 1 Y By Maclaurin S Theorem Up To The Third Degree Term Sarthaks Econnect Largest Online Education Community

Find The Taylor Series Expansion For F X 1 X At X 2 Youtube

Solved 7 The Taylor Series Approximation For Log 1 Z Chegg Com
2 Maclaurin Series
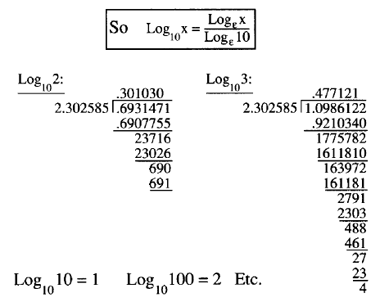
Logarithms Logs Log Ln Lg
Taylor Series From Wolfram Mathworld
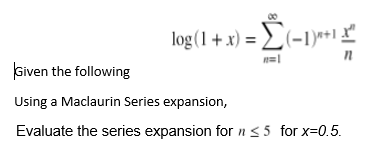
Solved Log 1 X Z 1 1 N Given The Following Us Chegg Com
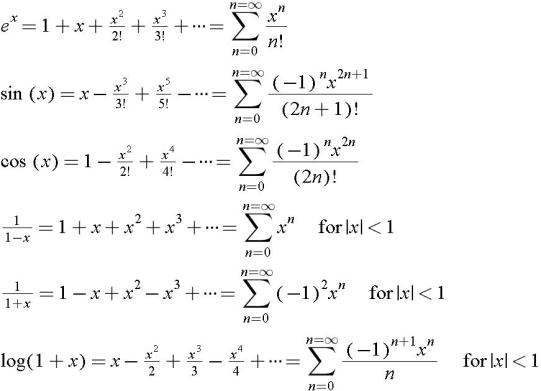
Appendix C Expansions Differentiation Integrals And Mathematical Relations Engineering360

Taylor Series Wikipedia
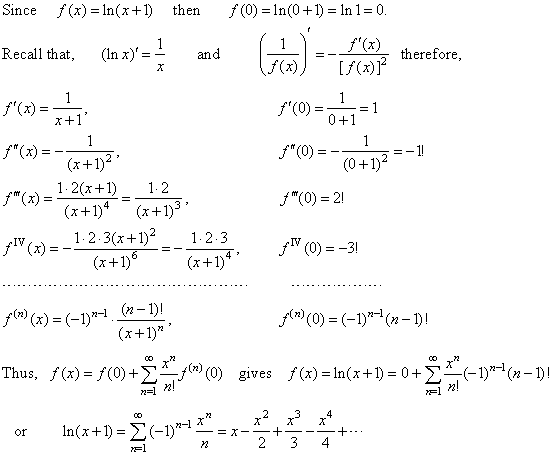
Maclaurin And Taylor Series Power Series Expansion Of Logarithmic Function

Natural Logarithm Series
What Is The Expansion Of Log 1 X Quora

Logarithms Logs Log Ln Lg

Taylor Series Wikipedia
Taylor And Maclaurin Series

Maclaurin Series For Ln 1 X How To Steps Video Lesson Transcript Study Com

Help With Arithmetic On Basic Taylor Series Expansion Mathematics Stack Exchange
Write The Maclaurin Series Expansion Of The Following Functions I E X Ii Sin X Iii Cos X Iv Log 1 X 1 X 1 Sarthaks Econnect Largest Online Education Community

Cochranmath Taylor Series Manipulation To Form New Series From Known Series

How To Find The Maclaurin Series Of 1 1 X Youtube

Maclaurin Series For Ln 1 X How To Steps Video Lesson Transcript Study Com
Taylor Series

Taylor Series Theorem Definition The Series Is Called The Taylor Series Of F About C Centered At C Ppt Download

Maclaurin Series For Ln 1 X How To Steps Video Lesson Transcript Study Com
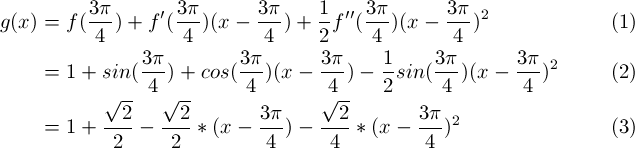
Taylor Series Tutorial By Chris Tralie

Consider The Following Two Taylor S Series Log 1 Chegg Com
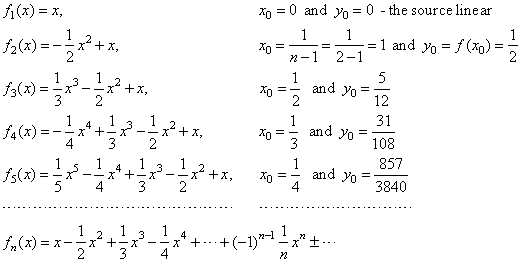
Maclaurin And Taylor Series Power Series Expansion Of Logarithmic Function

Finding Radius And Interval Of Convergence Of A Taylor Series Krista King Math Online Math Tutor

Video 2797 Maclaurin Series Ln 1 X 1 X Practice 1 2 Youtube

Expansion Of Functions Expansion Of Functions The Calculus Primer

Madhav University Maclaurin S Theorem

Expand Log Sec X By Maclaurin S Theorem Scholr
Expand Log 1 E X In Ascending Powers Of X Up To The Term Containing X 4 Sarthaks Econnect Largest Online Education Community

Taylor Series
Taylor Series For Log X Physics Forums
Www3 Nd Edu Apilking Math Lectures 32 Taylormclaurinseries Pdf

Power Series Taylor S And Maclaurin S Series

Maclaurin Series For Ln 1 X Youtube

Logarithms Logs Log Ln Lg

Power Series Taylor S And Maclaurin S Series

Natural Logarithm Series

Example Obtain The Maclaurin S Expansion For Ppt Video Online Download

Taylor Series Wikipedia
1
Logarithms Logs Log Ln Lg

Madhav University Maclaurin S Theorem

Finding Radius And Interval Of Convergence Of A Taylor Series Krista King Math Online Math Tutor

Maclaurin Series For Ln 1 X How To Steps Video Lesson Transcript Study Com

What Is The Correct Radius Of Convergence For Ln 1 X Mathematics Stack Exchange

The Maclaurin Series For Ln 1 X Is Given By X X 2 2 X 3 3 X 4 4 1 N 1 X N N Brainly Com
Edumatth Weebly Com Uploads 1 3 1 9 Taylor Series Pdf

The Natural Logarithm And Its Series Expansion 2 Ways Ln X 1 At 0 Youtube

Solved 1 Consider The Following Two Taylor S Series Log Chegg Com

Taylor Series

Natural Logarithm Wikipedia

Maclaurin Expansion For 1 Sqrt X 2 9 Mathematics Stack Exchange

Cochranmath Taylor Series Of A Function By Equating Derivatives

Taylor Series Numerical Methods Projects

What Is The Correct Radius Of Convergence For Ln 1 X Mathematics Stack Exchange

Taylors And Maclaurins Series Mathematical Relations Mathematical Concepts

The First 4 Terms Of The Maclaurin Series For Frac X Sin X Mathematics Stack Exchange

Taylor Series Wikipedia
How Do You Do The Taylor Expansion For F X Log X 1 At X 0 Socratic

Solved A Prove That The Taylor Series Of The Function F Chegg Com

Taylor Series Expansions Of Logarimathic Functions

Taylor Series With Max Bound On Error Of Logarithmic Function Youtube
Edumatth Weebly Com Uploads 1 3 1 9 Taylor Series Pdf



