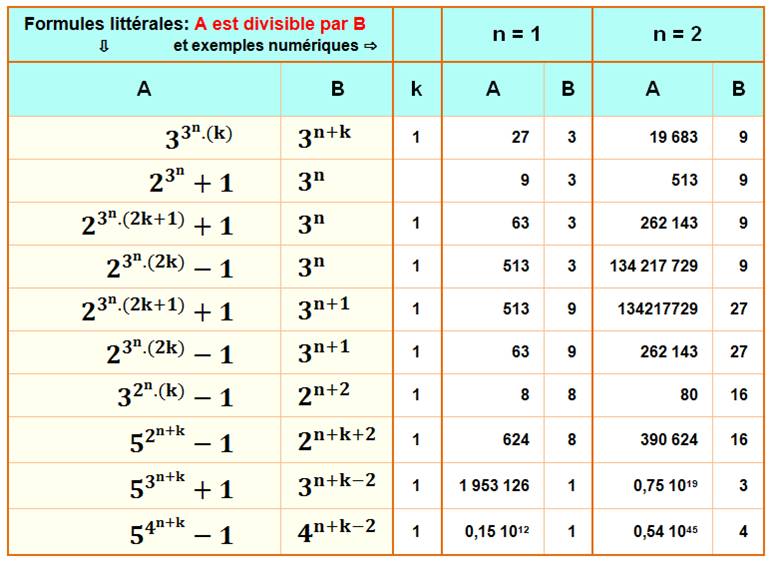
Nn+1n+2 Divisible Par 6

How To Prove That 4 N 15n 1 0 Mod 9 Quora

Le Petit Theoreme De Fermat Et N Puissance K Moins N
Oar Princeton Edu Jspui Bitstream 435 Pr1014r 1 What Probability That Random Integral 15 Pdf

9 Proof By Induction Sigma 9 N 2 N Is Divisible By 7 How To Use Mathgotserved Youtube

8 Proof By Induction S K 2 N N 1 2n 1 6 Discrete Principle Induccion Matematicas Youtube

Example 4 Prove That 7n 3n Is Divisible By 4 Chapter 4
Assuming the statement is true for n = k:.
Nn+1n+2 divisible par 6. Use principle of induction. P(n) = 7^n + 2 And then Show that it holds for n=1:. Of every 3 consecutive integers, exactly ONE is a multiple of 3.
For the first problem, note that a number is divisible by 6 if and only if it is divisible by both 2 and by 3. Thus, P(either n or n+1 is a multiple of 3) = 2/3. Discussion In Example 3.4.1, the predicate, P(n), is 5n+5 n2, and the universe of discourse is the set of integers n 6.
P(1) = 7^1 + 2 p(1) = 9 So it works for 1;. Let t1 = 1 and tn+1 = (t2 n + 2)/2tn for n ≥ 1. For n = 1, the statement reduces to 1 = 1 2 3 6 and is obviously true.
+ ++ n n+1 (Call this statement P(n)) (Call this statement P(n)) (Call this statement P(n)). I have tried, let mathematical induction, let P(n) be the statement, then then n^9 - n is divisible by 9. N, n+1 and n+2.
The first element that you do is undo the superb element that were given tangled. \( U_n = n^2(n+1)(n-1) \) On remarque que n-1,n et n+1 sont trois entier consécutifs et donc l'un d'eux est divisible par 3. You could try induction but it becomes a bit messy.
Thus the result is true for n=2, n=3, etc. N(n+1)(2n+1) = 6, divisible by 6. N(n+1)(n+2) divise 3 démonstration cas par cas دروس الجذع مشترك :.
Thus , it is true for n = 1 So , P 1 is true. Then I assumed that the original statement "11^(n+1)+12^(2n-1)is divisible by 133". Check whether P(3) and P(4) is true.
Consider three consecutive integers:. The form is straightforward. Write (Induction Hypothesis) say “Assume ___ for some 𝑘≥𝑎”.4.
Thanks This question is from textbook Intro to Real Analysis Found 2 solutions by aaaaaaaa, mathslover:. Prove by induction that n(n+1)(n+2) is divisible by 6 for n=1,2. So the question now becomes ‘Show that among n, n+2 and n+1’ one and only one is divisible by 3 i.e.
Consider what makes a number divisible by 6:. KhushiMidha KhushiMidha 07.07.18 Math Secondary School +5 pts. ) Hence ( n(n+1)(n+2) ) must be divisible by ( 24.
Giving nn(n+1)(n+2) is divisible by 6. Since n, n+1, n+2 are three consecutive integers, one of them is divisible by 3. Then what is the first number in the series?.
In this 1.2.3 represent the first term and 2.3.4 represent the second term. Is 216 divisible by 3?. Write (Base Case) and prove the base case holds for n=a.
For n(n+1) to be a multiple of 3, either n or n+1 must be a multiple of 3. Now let n = m be divisible by 7. Assume that P(k) is.
I do not understand it. In a series of numbers , the next number is formed by adding 1 to the sum of the previous numbers, and the 10th number is 1280. Es facil ver que n + (n + 1) + (n + 2) = 3(n + 1), de donde para que sea divisible por 6, necesariamente el factor (n + 1) debe ser un n´umero impar para cualquier n natural, lo que es falso.
(7) we will prove that the statement must be true for n = k + 1:. To prove that it is also true for n= k+1 if we assume it is true for n=k. For n = 1, we get 2^3 + 3^3 = 8 + 27 = 35;.
We have also shown that the results is true when n=1. Answered Prove that n(n+1)(n+2) is divisible by 6 1. N, n+1, and n+2 are 3 consecutive integers.
Thus, P(n+2 is a multiple of 3) = 1/3. Then, k(k+1)(2k+1) is divisible by 6. To sparkling up those variety of issues, get each and each of the letters on one area of the equation and the numbers on the different.
Por lo tanto, p(n) :. I.e k (k+1) (k+2) is a multiple of. Imagine of the challenge like a knotted up ball of string.
, divisible par 6 (ou prendre ) recurrence:. 1 + 3 + 6 + 10 + + (k + 1)(k + 2) 2 = (k + 1)(k + 2)(k + 3. Get 1:1 help now from expert Advanced Math tutors.
This is because n+4 = (n+1) + 3. On suppose à un rang n que divisible par 6:. If P(n) is the statement ‘2 2n – 1 is multiple of 3’ then show that P(5) is true.;.
For the second problem, we can solve this using modular arithmetic. Theory As per Euclid’s Division Lemma If a and b are 2 positive integers, then a = bq + r where 0 ≤ r < b If b = 3, a = 3q + r where 0 ≤ r < 3 So, r = 0, 1, 2 ∴ Numbers = 3q + 0, 3q + 1, 3q + 2 Let’s assume n = 3q, 3q + 1, 3q + 2 Now, we check whether n, n + 2, n + 4 is divisible by 3 If. Get an answer for 'how can I proof that n(n+1)(n+2)(n+3) is divisible by 24.
If n is odd, (n+1) should be divisible by 8 for the product to be divisible. N = 3q+r for some integer quotient q and remainder r in {0, 1, 2} If r=0 then n is divisible by 3 If r=1 then n+2 is divisible by 3 If r=2 then n+1 is divisible by 3 So at least (in fact exactly) one of n, n+1 and n+2 will be divisible by 3. Or the fact that the product of 3 consecutive numbers is divisible by 3.
Si vous ne comprenez pas le raisonnement, prenez les exemples suivants:. On the other hand n2(2n2-1) = 1(21-1) = 1.Thus the statement is true when n = 1. ) This will be true for any even number ( n.
This is an induction question and I really don't understand it.' and find homework help for other Math questions at eNotes. + (4n – 2) = 2n^2 is true. The last thing you need to do is show n(n+1)(n-1)(n+2) is divisible by 3.
Q-6 in the image Prove 10th by mathatical induction Prove by using the principle of mathematical induction 3 2n – 1 is divisible by 8 for n N. That's the order of operations -- parentheses, exponents, multiplication. For n+1 we have 7ⁿ⁺¹+2=7×7ⁿ+14−12 =7(7ⁿ+2)−12 =7×multiple of 3 −multiple of 3.
State the claim you are proving. Prove that 21 divides 4n+1 + 52n 1 whenever n is a positive integer. N (n+1) (n+2) =1 (1+1) (1+2) =6 hence true for n=1.
1 + 3 + 6 + 10 + + k(k + 1) 2 = k(k + 1)(k + 2) 6;. To Prove with mathetmatical induction that 7^n+2 is divisible by 3. Please please please help.
Let P(n) = 5 2n+2 – 24n – 25 is divisible by 576 For n = 0,P(0) = 5 2-25 = 25-25 = 0. 1.2.3 + 2.3.4 + … + n(n+1)(n+2). N(n+1)(n+2) is divisible by 6 for all nEN.
3 ^ (n+1) - 3 ^ (n-2) / 3 ^ (n-1) - 3 ^ (n+2) = ?. 96/8 = 12 possible numbers (n+1). The remainder that ‘n+4’ leaves on division by 3 will be the same as that left by ‘n+1’.
So answer could be 412/455. Total = 30 + 5 + 6 + 2 = 43. This means 2^(m+2) + 3^(2m+1) = 7·N, where N is a positive integer.
(d) Out of ( n ) and ( n+2, ) one is divisible by 2 and the other by ( 4, ) hence ( n(n+2) ) is divisible by ( 8. Click here 👆 to get an answer to your question ️ prove that n(n+1)(n+2) is divisible by 6 1. Page 1 of 3 Select Solutions Problem Set #9 1 Section 2.4 6(f) We first prove this for the case that n = 1.
2 points · 3 years ago. Multiple de 3, du coup le produit divise par 3 b. Homework Statement Prove by Induction the 11^(n+1)+12^(2n-1) is visible by 133.
1 1 (8) For all integers n > 0, prove that n - n is divisible by 6 (9) For all integers n > 1, prove:. In any three consecutive numbers, at least one will be even (a multiple of 2), and one will be a multiple of 3. 4 Applying other theorems about behavior of limits under arithmetic operations with sequences, we conclude that lim 1 2 q 1+ 1 4n +2 = 1 2·1+2 = 1 4.
So we can form a triangle in 455 - 43 = 412. = 30' and find homework help for other Math questions at eNotes. Prove the product of 4 consecutive integers is always divisible by 24 using the principles of math induction.
N+(n+1)+(n+2) = 6q, q ∈ N, es falso. N 2 + n is even. Let P(n) be the statement," n 3 + n is divisible by 3".
Let P(n) = n (n+1) (n+2) is an integral multiple of 5 for = 3, P(3. First thing I guess is to label the equation;. It has to be even (divisible by 2) and the digits add up to a multiple of 3.
Use Mathematical Induction to show that the statement 2 + 6 + 10 +. N(n+1)(n+2) divisible par 6 (le prouver par récurrence) et j'insiste bien sur le fait qu'ici, n+1 et n+2 ce sont pas des rangs par rapport au premier n, c'est à n on ajoute 1 puis dans le deuxième facteur 2. Let P k be also true.
If n is even, then the product is sure to be divisible by 8 (or three 2's) n is even so it is divisible by one 2. So k(k+1)(2k+1) =6m (1) Now to prove that the result is true for n=k+1. Il existe k relatif tel que donc 7^(n+1)-1-6=6*7*k 7^(n+1)-1=6*(7k+1) donc la condition est vrai au rang n+1, et il ne reste plus qu'à conclure.
For all n>1 or n=1 Homework Equations The Attempt at a Solution I have shown that the base case of n=1 holds. Prove that n^3 + (n+1)^3 + (n+2)^3 is divisible by 9 for all n in Natural numbers. Use Proof by Mathematical induction to prove that 7^n + 2 is divisible by 3 for all n in the Natural Numbers.
The answer is - 1/3. Assume that tn converges and find the limit. Mathematical Induction (Examples Worksheet) The Method:.
2^(m+3) + 3^(2m+3) = 2·2^(m+2) + 9. Okay this is my third question i am asking regarding a math. As any three consecutive integers will contain at least one multiple of 2 and exactly one multiple of 3, the product of any three consecutive integers will be divisible by both, and thus by 6.
Put n = 1, we get 6 1 + 2 + 7 2 + 1 = 216 + 343 = 559, which is divisible by 43. Let the statement be 7^n+2 is divisible by 3. Bonjour tout le monde Je viens de réaliser deux petites démos par récurrence, mais je bloque sur la troisième qui est la suivante :.
It is not easy to stumble upon the trick needed in the inductive step in this exercise, so do not feel bad if you did not nd it. Ask a New Question. 30 1.2.3 + 2.3.4 = 6 + 24 = 30 Input :.
The solution at the back like factorises it but i dont get it. If this is true, what can we conclude about n = m+1?. N (n+1) (n+2) is divisible by 6, then find P (3).
Sinon par récurrence de la même façon :. In this case, X1 i=1 (2i-1)3 = (2(1)-1)3 = 1:. Car soit n, soit n+1, soit n+2 divise par 3.
The correct answer is D. For the basis step (n = 1), we simply observe that 41+1 + 52(1) 1 = 16 + 5 = 21. Could anyone help me on this one?.
Assume it is true for n=k. Let us assume that 7ⁿ+2 is divisible by 3 for any n. Get an answer for 'Solve the expression ( n +1 )!/( n-1)!.
You MUST at some point use your. Thus we have proved that if n(n+1)(n+2) is divisible by 6 then (n+1)(n+2)(n+3) is divisible by 6. Déjà n(n+1)(n+2) divise par 3.
1.22.3 n(n+1) (10) For all integers n > 0, prove:. You can view more similar questions or ask a new question. One must be divisible by 3, since n=3r, where r is an integer, or n=3r+1 so n+2=3r+3 which is divisible by 3, or n=3r+2 so n+1`=3r+3 which is divisible by 3.
In every three consecutive natural numbers exactly one is divisible by 3. B Prove the following by using the principle of mathematical induction for all n∈N:. Prove the (k+1)th case is true.
N, n+1,n+2 are consecutive integers and at least one must be even. Yes, because the sum of 2 + 1 + 6 = 9, which is divisible by 3. The question can be presented as:.
Plz help me to solve do it step wise plz. Hence n(n+1)(n+2) will be divisible by 3 too. Question This question is from textbook Intro to Real Analysis:.
Question 13 Show that exactly one of the numbers n, n + 2 or n + 4 is divisible by 3. Expert Answer 100% (1 rating) Previous question Next question Get more help from Chegg. Prove that 6|7^n+4^n+1 when n is positive interger Let P(n) be the proposition that asserts 7^n+4^n+1 is divisible by 6.
Hypothesis n (n+1) (n+2) is a multiple of 6. (n+2) is divisible by 4 since it has two 2's. (Don’t use ghetto P(n) lingo).
7ⁿ+2 =7¹+2= 9 which is divisible by 3 Hence it is true for n= n. Let the result be true for n=k. (WITHOUT using induction, we have yet to get to induction so I figure it would be wise to do this without it.) Homework Equations /B The section we were given this under primarily talks about the quotient remainder theorem (n = dq+r) though I couldn't figure out how to apply this either.
I would use the division algorithm for this part, if you've learned it. 1 + 3 + 6 + 10 + + n(n+ 1) 2 = n(n+ 1)(n+ 2) 6 Proof:. Exercice d'introduction pour apprendre à faire un raisonnement par récurrenceDémontrer par récurrence que 1x2++n(n+1)=n(n+1)(n+2)/3Tout le cours et les exerci.
Prove n(n+1)(n+2) is divisible by 6 for all integers n. Find the sum up to n terms of the series:. Prove the product of 4 consecutive integers is always divisible by 24 using the principles of math induction.
P(1) is true, since 7+4+1 = 12, 6|12 Inductive step:. +n(n+1)= n(n+1)(n+2)/2 using the mathematical induction. Since n and n+1 are two consecutive integers, one of them is divisibly by 2.
9 is divisible by 3. Thus, by mathematical induction product of three consecutive natural numbers is divisible by 6. La suma de 3 enteros consecutivos no es necesariamente divisible por 6.
MATHEMATICAL INDUCTION Which shows 5(n+ 1) + 5 (n+ 1)2.By the principle of mathematical induction it follows that 5n+ 5 n2 for all integers n 6.

Pdf Wolstenholme S Theorem Its Generalizations And Extensions In The Last Hundred And Fifty Years 1862 12

Induccion Matematica
Http Www Isical Ac In Sush Discrete Maths 14 Principle of inclusion and exclusion Pdf

Math Origins

Le Petit Theoreme De Fermat Et N Puissance K Moins N

Nombre De Bernoulli Wikipedia
Http Citeseerx Ist Psu Edu Viewdoc Download Doi 10 1 1 177 15 Rep Rep1 Type Pdf
Www Maths Nottingham Ac Uk Plp Pmzcw Download Aln3 Pdf

19 Prove Induction N 3 N Is Divisible By 3 Mathgotserved Mathematical Precalculus Discrete Princ Youtube
2

Lecture Notes In Discrete Mathematics
How To Prove That 4 N 15n 1 0 Mod 9 Quora

Prove That For Every Value Of N N 4 2 N N Help Pls Askmath

Ts Spe Maths 11 Divise 4 4n 2 3 3n 3 Congruence Et Divisibilite Youtube
Www Fq Math Ca Issues 12 3 Pdf

5 Principle Of Mathematical Induction N3 2n Is Divisible By 3 Discrete N 3 2n Pt Viii Mathgotserved Youtube
Http Lewebpedagogique Com Larenedesmaths Files 10 12 Ds2 Spe 10 11 Corr Pdf

Catalan Number Wikipedia
Oar Princeton Edu Jspui Bitstream 435 Pr1014r 1 What Probability That Random Integral 15 Pdf

Pdf The Arithmetic Derivative And Antiderivative
Oar Princeton Edu Jspui Bitstream 435 Pr1014r 1 What Probability That Random Integral 15 Pdf
Pdf4pro Com File 9d4d2 257ethomas Courses Texts1 21 Pdf Pdf

Prove That N N 1 N 2 Is Divisible By 6 Principle Of Mathematical Induction Youtube

Ex 4 1 21 Prove X2n Y2n Is Divisible By X Y Class 11
Q Tbn 3aand9gcszufvm Pdipk6b3vmxyywgp Wz3d X6krztdfhx08dvg8zfga Usqp Cau

Prove That N 3 N Is Divisible By 6 Euclid Division Lemma Youtube

N N 1 N 2 Divise 3 Youtube
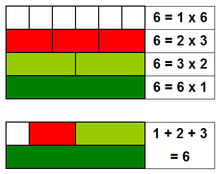
Formes Divisibles Par Un Nombre

Ex 8 1 13 Show That 9n 1 8n 9 Is Divisible By 64

Theorie Des Nombres Pairs Et Impairs

X 4x 7x 3n 2 X 1 2n 3n 1 X X 4x 7x 3 N 2 X N 3n 1 Xx

Divisibilite Dans Z Division Euclidienne Exercices Resolus

Le Petit Theoreme De Fermat Et N Puissance K Moins N

Divisibilite De Carre Plus Un

Ism Et Chapter 8

Ex 8 1 13 Show That 9n 1 8n 9 Is Divisible By 64

Rappel N N N 1 N 2 X 2 X 1

Prove That N N 1 N 2 Is Divisible By 6 Principle Of Mathematical Induction Youtube
Perfect Number Wikipedia

Criteres De Divisibilite Caracteres Generaux
Math Mit Edu Research Highschool Rsi Documents 17puig Pdf
Www Risc Jku At Publications Download Risc 5338 Dancingsambaramanujan Pdf
Arxiv Org Pdf 1003 4015

Mathematical Induction Prove That 7 N 3 N Is Divisible By 4 Youtube

Le Petit Theoreme De Fermat Et N Puissance K Moins N
Http Www Flashmath Fr Scholatech Bases S1554 Pdf
Math Mit Edu Research Highschool Rsi Documents 17puig Pdf

Factorial Wikipedia

Example 4 Prove That 7n 3n Is Divisible By 4 Chapter 4

Induccion Matematica
Http Www Csun Edu Asethura Giaafiles Giaav2 01 T Giaav2 01 T Pdf

Corriges Des Exercices
Faculty Math Illinois Edu Nirobles Files453 Practicemidterm1solutions Pdf

Proof Of N N 2 5 Is Divisible By 6 For All Integer N Ge 1 By Mathematical Induction Mathematics Stack Exchange
Http Www Math Ucsd Edu Ronspubs 76 12 Factorial Products Pdf

7 2n 2 3n 3 3 N 1 Is Divisible By 25 For Any Natural Number N 1 Prove That By Mathematical

Ism Et Chapter 8

Exercices

Using Mathematical Induction To Prove 2 3n 3 N Is Divisible By 5 Youtube

Prove That 10 N 3 4 N 2 5 Is Divisible By 9 By Principle Of Mathematical Induction Plz Plz Plz Brainly In

If N 2 Is Even Then N Is Even Chilimath
Math Mit Edu Research Highschool Rsi Documents 17puig Pdf
Ir Cwi Nl Pub d Pdf

17 Proof Prove Induction 8 N 1 Is Divisible By 7 Divides Youtube
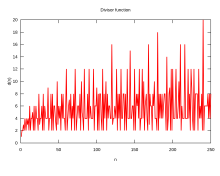
Divisor Function Wikipedia
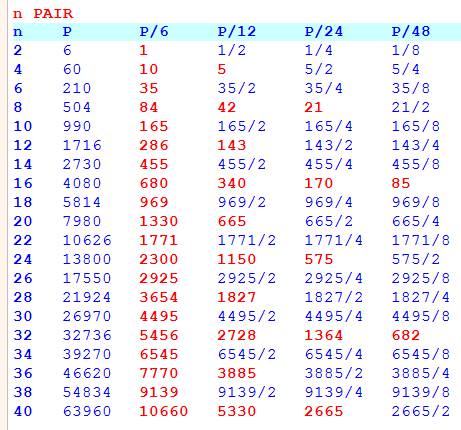
Divisibilite Produit Trois Nombres Consecutifs Suite
Http Faculty Atu Edu Mfinan Main2 Pdf

Matiere Mathematiques Revision Arithmetique Dans In Ensembles De Nombres

Prove That N 3 N Is Divisible By 6 Youtube

Lecture Notes In Discrete Mathematics
Arxiv Org Pdf Math

Rd Sharma Solutions For Class 10 Chapter 9 Arithmetic Progressions Get Free Pdf

Ex 4 1 6 1 2 2 3 3 4 N N 1 N N 1 N 2 3

Proof That N 3 N Is Divisible By 3 Using Mathematical Induction Youtube

Three Math Puzzles Inspired By John Horton Conway Quanta Magazine

Ex 4 1 Prove 102n 1 1 Is Divisble By 11 Chapter 4

Prove Using Mathematical Induction That 2 3n 3 N Is Divisible By 5 For All N 1 Mathematics Stack Exchange
Http Www Math Evry Cnrs Fr Media Members Ihonore Td1 1617 Arithm Z Pdf
Http Www Math Mit Edu Rstan Bij Pdf
Search Q 1 5e2 2b2 5e2 2b3 5e2 2b 2bn 5e2 Formula Tbm Isch
Q Tbn 3aand9gcretul7zulk4jjt2zmct06tak9w Jnzszoywthmbsa Usqp Cau
Arxiv Org Pdf 14 1450
Math Mit Edu Research Highschool Rsi Documents 17puig Pdf

Prove That N N 1 N 2 Is Divisible By 6 Principle Of Mathematical Induction Youtube
Http Www Math Utoronto Ca Barbeau Olymon03 Pdf
N 2 N 1 2 4
Prime Number Wikipedia

Example 4 Prove That 7n 3n Is Divisible By 4 Chapter 4

Exercices D Arithmetiques Ppt Video Online Telecharger

Collection De Nombres Divisibilite Par 6
Http Math Slu Edu Clair Mcmc Floor Solutions Pdf

Applications Du Pgcd Et Du Ppcm

Math Olympiad Problems Collection V1 Colecao De Problemas De Matematica De Todo Docsity

Pdf Counting Square Free Numbers
Dsury Com Content Images Books 113 Fraleigh Soln Pdf

Induccion Matematica
Http Www Southalabama Edu Mathstat Personal Pages Jbarnard Archive Teaching S12 3 Test2sol Pdf

Key Triangle Numbers



