Power Series Expansion Of Log1+x

Solved Find The Following Limit Lim X Rightarrow 0 Ln 1 Chegg Com
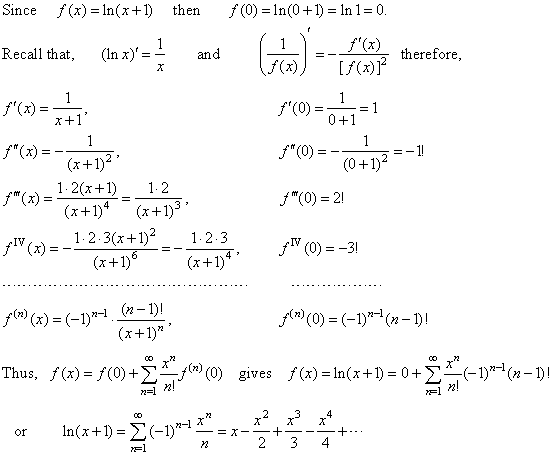
Maclaurin And Taylor Series Power Series Expansion Of Logarithmic Function

Power Series Taylor S And Maclaurin S Series

Taylor Series For F X Ln X Centered At X 1 Youtube
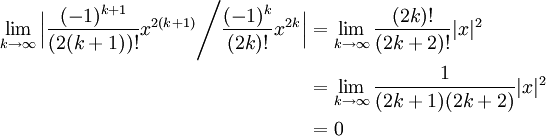
The Maclaurin Expansion Of Cos X The Infinite Series Module

Ap Calculus Review Taylor And Maclaurin Series Magoosh Blog High School
F ′ (x) = 1 (1 − x) 2.
Power series expansion of log1+x. E(17x) = P 1 n=0 (17 x)n!. Consider the function of the form \f\left( x \right) From basic to higher mathematics. Given translated logarithmic function is the infinitely differentiable function defined for all - 1 < x < oo.
The natural logarithm of a number is its logarithm to the base of the mathematical constant e, where e is an irrational and transcendental number approximately equal to 2.718 281 8 459.The natural logarithm of x is generally written as ln x, log e x, or sometimes, if the base e is implicit, simply log x. Expansion of logarithmic series. We have 1 (1−x)2 d dx 1 1−x and 1 1−x X∞ n=0 xn, hence 1 (1−x)2 d dx X∞ n=0 x n= X∞ n=0 d dx xn = X∞ n=1 nx −1 = 1+2x+3x2 +4x3 +··· = X∞ n=0 (n+1)xn (re-indexed)The radius of convergence is R = 1.
F(x) = e x. Actually, just to give ourselves some closure here, let's write it in sigma notation. Introduction A power series (centered at 0) is a series of the form ∑∞ n=0 anx n = a 0 +a1x+a2x 2.
Find a power series representation for tan−1 x. Expansion of log e (1 + x) if |x|<1 then Replacing x by −x in the logarithmic series, we get. Differentiating it again simply increases the power as you can see.
That function is the antiderivative of 1/(1+x2. 1 (1 x)2 = d dx 1 1 x = d dx " X1 n=0 xn # = X1 n=0 d dx xn = X1 n=1 nxn 1 = 1 + 2x+ 3x2 + 4x3. Deriving the Maclaurin expansion series for ln(1+x) is very easy, as you just need to find the derivatives and plug them into the general formula.
For Teachers for Schools for Working Scholars® for. An expansion for log e (1 + x) as a series of powers of x which is valid only, when |x|<1. And so the power series expansion agrees with the Taylor series.
Series (sin z)/z. It is also the radius of the circle in the complex plane within which the. Power series expansion for logarithmic terms:.
A power series $\displaystyle\sum_{n=0}^\infty c_n x^n$ can be thought of as a function of $x$ whose domain is the interval of convergence. How do you go about deriving the series expansion of ln(x)?. HOWEVER, we must do more work to check the convergence at the end.
If a function \(f\left( x \right)\) has continuous derivatives up to \(\left( {n + 1} \right)\)th order inclusive, then this function can be expanded in a power series about the point \(x = a\) by the Taylor formula:. By method of power series expansion, find the inverse z-transform of the following 1 X(z) = log(1 – 2z), Iz| < 2 Get more help from Chegg Get 1:1 help now from expert Electrical Engineering tutors. However, use of this formula does quickly illustrate how functions can be represented as a power series.
Find more Mathematics widgets in Wolfram|Alpha. Note this is the geometric series. + x8 8.
By signing up, you'll get thousands of step-by-step. X 2R cosx = 1 x2 2!. Parentheses are sometimes added for clarity, giving ln(x), log e (x), or log(x).
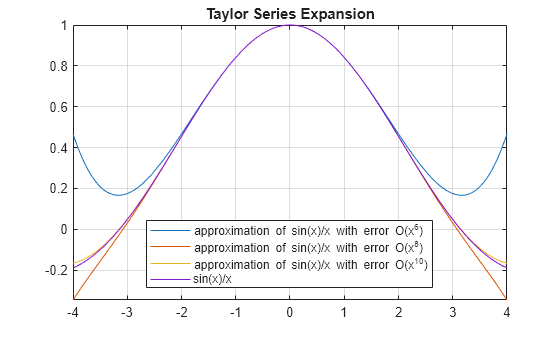
To find the power series for ln(1 - x) we. = X1 n=0 17n n n!. Let' s make use of Mathematica to see how well the series expansion represents f(x) = 1/(1 - x).
Get the free "Log(1-x) Taylor Series" widget for your website, blog, Wordpress, Blogger, or iGoogle. = X1 n=0 xn n!. If you're seeing this message, it means we're having trouble loading external resources on our website.
Whether the series converges or diverges, and the value it converges to, depend on the chosen x-value, which makes power series a function. By using this website, you agree to our Cookie Policy. Series Expansion of Exponential and Logarithmic Functions.
Free math lessons and math homework help from basic math to algebra, geometry and beyond. Once you differentiate, you end up with a simple reciprocal. A power series about a, or just power series, is any series that can be written in the form, \\sum\limits_{n = 0}^\infty {{c_n}{{\left( {x - a} \right)}^n}} \ where \(a\) and \({c_n}\) are numbers.
Second, being able to create power series allows us to define new functions that cannot be written in terms of elementary functions. The function z 1 is analytic on Cnf0g˙D jz0j(z0):. The exponential function is the infinitely differentiable function defined for all real numbers whose.
Power series is a sum of terms of the general form aₙ(x-a)ⁿ. Consider the function of the form \f\left( x \right) = \sqrt {1 + x} \. What is the binomial expansion for (1+x)^-1?.
Free Taylor/Maclaurin Series calculator - Find the Taylor/Maclaurin series representation of functions step-by-step This website uses cookies to ensure you get the best experience. Let's see what happens if we compare the plots of f(x)=1/(1-x) with the plots of the series expan-. -1)"+1 log(1+x)= Question # 2 (25 pts.):.
Function f(x) = 1/(1 - x), or any other function like cos x or arc tan x can be accurately approxi-mated by an infinite sum of powers of x?. Multivariate Taylor series is used in many optimization techniques. Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
The Taylor series for log(1 - x) is the same except that *all* of the terms are negative rather than alternating. The power series expansion of the exponential function Let represent the exponential function f (x) = e x by the infinite polynomial (power series). Finding the Power Series for ln(1 - x) A power series is the sum of an infinite number of terms.
Functions as Power Series. Series expansions of exponential and some logarithms functions. Power Series Power series are one of the most useful type of series in analysis.
Students, teachers, parents, and everyone can find solutions to their math problems instantly. For the function itself. Note that d dx 1 1 x = 1 (1 x)2 and we know what the power series representation of 1 1 x.
Series exp(1/x) at x = infinity;. In this tutorial we shall derive the series expansion of $$\sqrt {1 + x} $$ by using Maclaurin's series expansion function. Since every polynomial function in the sequence, f 1 (x),.
Commonly Used Taylor Series series when is valid/true 1 1 x = 1 + x + x2 + x3 + x4 + :::. Each term is a power of x multiplied by a coefficient. Find a power series of f(x) = 1/(1+x)^3 and find the interval of convergence.
Seriesf, {x, x0, n} generates a power series expansion for f about the point x = x0 to order (x - x0) n, where n is an explicit integer. E = 1 + 1 + 1 2!. REPRESENTATION OF FUNCTIONS AS POWER SERIES 100 Answer:.
The power series expansion of logz about z0 has radius of convergence R = jz0j, for z0 6= 0, and any branch of logz. The even power terms will remain negative when -x is raised to an even power, but the odd power terms will become negative when -x is raised to an odd power. Just replace x with -x in the series for log(1 + x);.
⇐ Maclaurin Series of ln(1-x). It's been a while since i did calc. Proof.The radius of convergence for logz about z0 is the same as the radius of convergence for its derivative, (logz)0= z 1.
The Taylor series for the exponential function ex at a = 0 is The above expansion holds because the derivative of e xwith respect to x is also e and e0 equals 1. Power series expansion of tan(x), Dividing power series, maclaurin series of tan(x), how to divide power series, blackpenredpen. Seriesf, x -> x0 generates the leading term of a power series expansion for f about the point x = x0.
Some Important results from logarithmic series. Exponential and Logarithmic Function and Series,Expansion of e^x,a^x and log(1+x) xx. The Maclaurin series for 1 / 1 − x is the geometric series.
By using this website, you agree to our Cookie Policy. For any branch of logz, its power series expansion at z0 is log(z0) +. Exponential Function:The function which is in the form of $$\;y=f(x)=a^x,\;\;\;\;\;a>0$$ is called an exponential function in which the base a is constant and the power or index x is a variable.
X1n = 0.3" un x2n = an -0.3 an-1 and x3n is obtained by convolving xin and x2n that is x3n = x1n * x2n * x2n a) Find the complex cepstrum, î;(n). Just think of x as r = X1 n=0 xn x 2( 1;1) ex = 1 + x + x2 2!. (1 + x) 3 = 1 + 3 x + 3 x 2 + x 3 (1+x)^3 = 1+3x+3x^2+x^3 (1 + x) 3 = 1 + 3 x + 3 x 2 + x 3, f (x) f(x) f (x) cannot be, so there cannot be a finite sum of monomial terms that equals f (x) f(x) f (x).
Series (sin x)/(x - pi) at x = pi to order 10;. Usually, a given power series will converge (that is, approach a finite sum) for all values of x within a certain interval around zero—in particular, whenever the absolute value of x is less than some positive number r, known as the radius. For example, we can use them to define transcendental functions such as the exponential and trigonometric functions (and many other less familiar functions).
And the corresponding Taylor series for log(x) at a = 1 is and more generally, the corresponding Taylor series for log(x) at some is:. But there is a way to recover the same type of expansion if. In this tutorial we shall derive the series expansion of the trigonometric function $${a^x}$$ by using Maclaurin's series expansion function.
The \({c_n}\)’s are often called the coefficients of the series. Expansions at generic point z==z 0. The interval of convergence is the open, closed, or semiclosed range of values of x x x for which the Maclaurin series converges to the value of the function;.
Power series, in mathematics, an infinite series that can be thought of as a polynomial with an infinite number of terms, such as 1 + x + x 2 + x 3 +⋯. The radius of convergence stays the same when we integrate or differentiate a power series. Free power series calculator - Find convergence interval of power series step-by-step This website uses cookies to ensure you get the best experience.
Laurent series cot z;. To use the Geometric Series formula, the function must be able to be put into a specific form, which is often impossible. Thus a function is analytic in an open disk centred at b if and only if its Taylor series converges to the value of the function at each point of the disk.
Taking the derivative of the MacLaurin series gives you $1 -x +x^2 - x^3 + x^4 + \ldots$ Since this is a geometric series with ratio $-x$, it equals $\frac{1}{1 + x}$ when x is in $(-1, 1)$. As you can see ln1 = 0. Following is a list of examples related to this topic—in this case, different kinds and orders of series expansions.
The first thing to notice about a power series is that it is a function of \(x\). Maclaurin series cos(x) taylor series sin x;. Is there a function we know of that has a power series representation and can be di er-entiated or integrated to give us 1 (1 2x).
The power series expansion of the logarithmic function Let represent the translated (shifted) logarithmic function f (x) = ln (x + 1) by the power series. Series » Tips for entering queries. Determine the Taylor series at x=0 for f(x) = e x.
In this section we discuss how the formula for a convergent Geometric Series can be used to represent some functions as power series. The sum of partial series can be used as an approximation of the whole series. Outside the domain, the Maclaurin series either is undefined or does not relate to the function.
The radius of convergence is half the length of the interval;. Problems on Taylor’s Theorem. We use the polynomial with infinitely many terms in the form of power series.
This shows the expression $\ln(1+x)$ and its MacLaurin expansion to have the same derivative over $(-1, 1)$, which means they are equal within a constant. For example, given the power series representation for f (x) = 1 1 − x, f (x) = 1 1 − x, we can find a power series representation for f ′ (x) = 1 (1 − x) 2. Natural log of one plus x to the third power is x to the third power minus x to the sixth over two plus x to the ninth over three, so on and on and on.
The answer is yes.
Write Down The Taylor Series Expansion Of The Function Log X About X 1 Upto Three Non Zero Terms For X 0 Sarthaks Econnect Largest Online Education Community
Www Uio No Studier Emner Matnat Math Mat4270 H12 Notes5 0 Pdf
Taylor Series Matlab Taylor
Exponentiated Power Generalized Weibull Power Series Family Of Distributions Properties Estimation And Applications
The Power Series Expansion Of The Logarithmic Function Properties Of The Power Series Expansion Of The Logarithmic Function The Binomial Series
The Power Series Expansion Of The Logarithmic Function Properties Of The Power Series Expansion Of The Logarithmic Function The Binomial Series
2
Math Mit Edu Jorloff 18 04 Notes Topic7 Pdf
Www Maths Ox Ac Uk System Files Legacy W8 Trudgian Pdf

Taylor Series Expansions Of Logarimathic Functions

Series Expansion Calculator Wolfram Alpha
Projecteuclid Org Download Pdf 1 Euclid Tjm

Exponential And Logarithmic Function And Series Expansion Of E X A X And Log 1 X Notes Videos Qa And Tests Grade 12 Mathematics Binomial Theorem Kullabs

Find Expansion Of Log 1 Tanx Youtube

Taylor Series Expansions Of Exponential Functions

In Maclaurin Series Of Sin2x The Coefficient Of The Third Term Is

Problem 5 Equation 1 Is The Infinite Taylor Series Expansion Of Ln 1 X Where In Is The Natur Homeworklib

Power Series Taylor S And Maclaurin S Series

A Expansion In The Power Series Of Ln 1 X According To The Download Scientific Diagram

Taylor Series Wikipedia

Taylor Series Wikipedia
Taylor And Maclaurin Series
The Power Series Expansion Of The Logarithmic Function Properties Of The Power Series Expansion Of The Logarithmic Function The Binomial Series
1
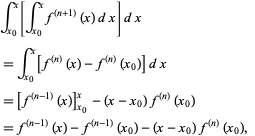
Taylor Series From Wolfram Mathworld

Taylor Series Wikipedia

Pdf Expansions Of The Exponential And The Logarithm Of Power Series And Applications
Q Tbn 3aand9gcqhsqudeodhcaoqaod4 Olimsxzqrk5xb2ok 91wui0kjggwboa Usqp Cau
Http Citeseerx Ist Psu Edu Viewdoc Download Doi 10 1 1 493 2397 Rep Rep1 Type Pdf
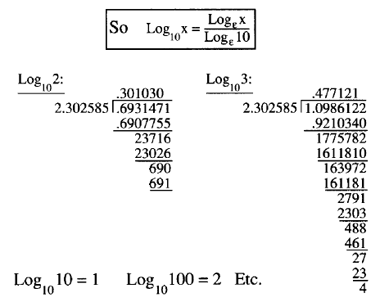
Logarithms Logs Log Ln Lg

C Exercises Calculate E Raise To The Power X Using Sum Of First N Terms Of Taylor Series W3resource

Expansion Of Log 1 X Maclaurin Series Youtube
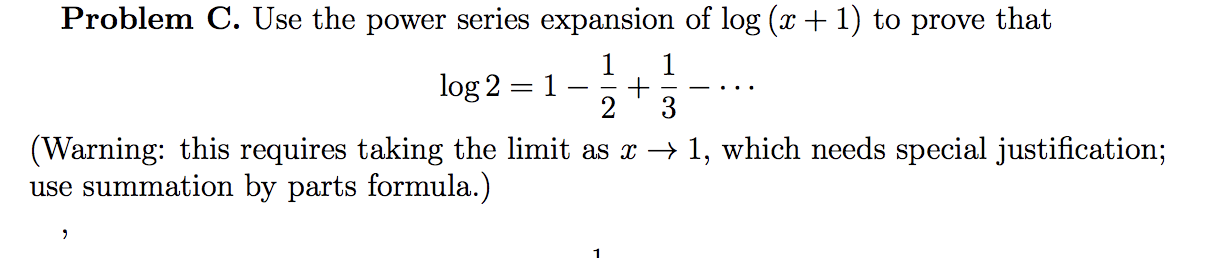
Solved Problem C Use The Power Series Expansion Of Log Chegg Com
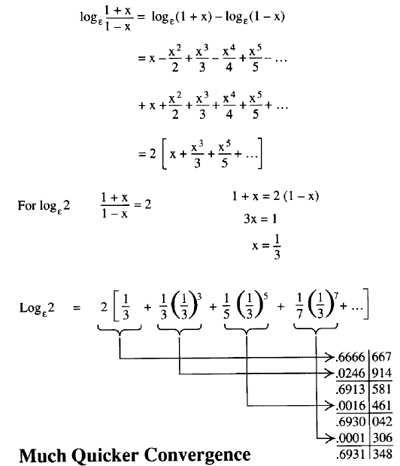
Logarithms Logs Log Ln Lg

Taylor Series Wikipedia
Http Citeseerx Ist Psu Edu Viewdoc Download Doi 10 1 1 512 5433 Rep Rep1 Type Pdf

Taylor Series Expansions Of Inverse Hyperbolic Functions
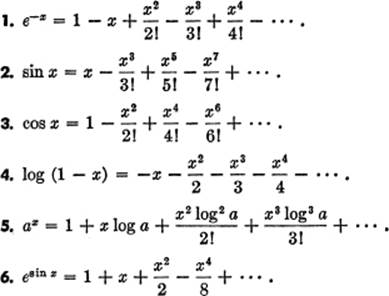
Expansion Of Functions Expansion Of Functions The Calculus Primer

Digital Signal Processing Part2

Maclaurin Series For Ln 1 X Youtube

Taylor Series Wikipedia

Problem 4 Using The Taylor Series Representation Of Logz From The Last Part Of Problem 3 Show T Homeworklib
The Power Series Expansion Of The Logarithmic Function Properties Of The Power Series Expansion Of The Logarithmic Function The Binomial Series

2 Question By Method Of Power Series Expansion Chegg Com

Taylor Series
How To Expand Log 1 Log 1 X In Powers Of X As Far As X 4 Quora

Logarithms Logs Log Ln Lg
Math Mit Edu Jorloff 18 04 Notes Topic7 Pdf
Projecteuclid Org Download Pdf 1 Euclid Bams

Ap Calculus Review Taylor And Maclaurin Series Magoosh Blog High School
Expand Log 1 E X In Ascending Powers Of X Up To The Term Containing X 4 Sarthaks Econnect Largest Online Education Community

Natural Logarithm Wikipedia
1
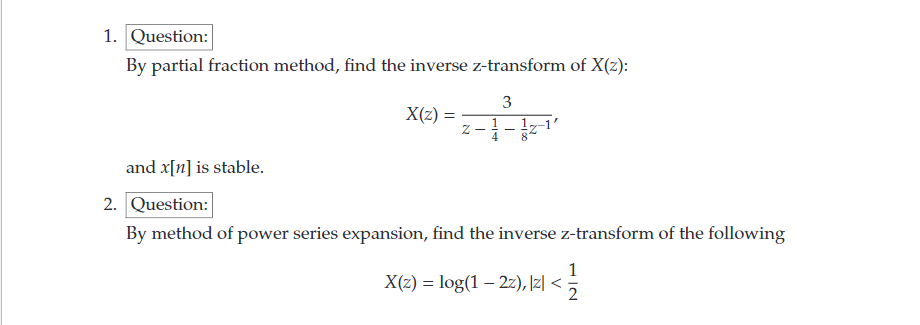
Solved 1 Question By Partial Fraction Method Find The I Chegg Com

Problem 5 Equation 1 Is The Infinite Taylor Serie Chegg Com

Power Series Expansion Of Log X Power Series In Bengali Youtube

Maclaurin Expansion Of Ex The Infinite Series Module

Logarithms Logs Log Ln Lg

Solved 1 Find The Power Series Expansion Of F X Z Chegg Com
What Is The Expansion Of Log 1 X Quora
Q Tbn 3aand9gctlcjugshanpv Xexyyrw4nyaxmkw0djgyjfessp7xhb6sqgy1x Usqp Cau

Taylor Series Wikipedia
Infinite Sequences And Series Ap College Calculus Khan Academy

Natural Logarithm Wikipedia
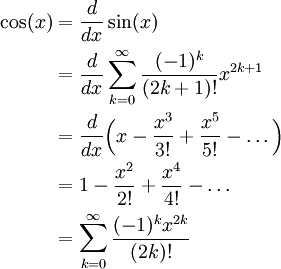
The Maclaurin Expansion Of Cos X The Infinite Series Module
How To Expand Log 1 Log 1 X In Powers Of X As Far As X 4 Quora
Http Academic Uprm Edu Wrolke Esma6661 Hyp1 Html

Power Series Intro Video Khan Academy
Arxiv Org Pdf 1903

Find A B And N In The Expansion Of A B N If The First Three Terms Of The
What Is The Binomial Expansion Of Math 1 X 2 Math Quora
Expand Log X In Powers Of X 1 By Taylor S Series Sarthaks Econnect Largest Online Education Community

Index Power Series Tables

Taylor Series Wikipedia
Q Tbn 3aand9gcqdb9a Cnsdci2jcvt5d9edqlsboxtwdmthh Fiz15rljdrr8cr Usqp Cau

Index Power Series Tables

Power Series Taylor S And Maclaurin S Series

8 Prove That Dt 1 T N 1 For X E A A 0 A 1 And Deduce From There A Power Series Expansion For In 1 X 8 Prove That Dt 1 T N 1 For X E A A 0 Homeworklib

Taylor Series Wikipedia

1 7 Inversion By A Power
Old Renyi Hu P Erdos 1949 01 Pdf

Logarithms Logs Log Ln Lg

Math Tutor Series Methods Survey Function Series
2

Differentiating Power Series Video Khan Academy

Pdf Evaluation Of Apery Like Series Through Multisection Method
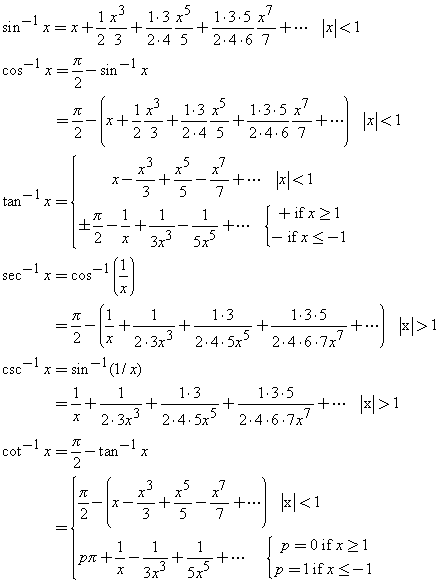
Taylor Series Expansions Of Inverse Trigonometric Functions
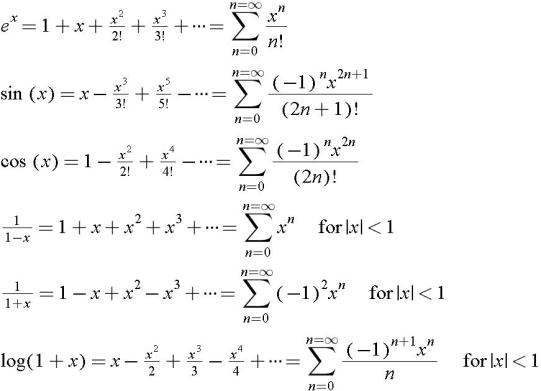
Appendix C Expansions Differentiation Integrals And Mathematical Relations Engineering360

Dc Response Discrete Time Fourier Transform X N X Ejw Ppt Download

Taylor Series Expansion Of Natural Log Function Youtube
Expand Log 1 E X In Ascending Powers Of X Up To The Term Containing X 4 Sarthaks Econnect Largest Online Education Community
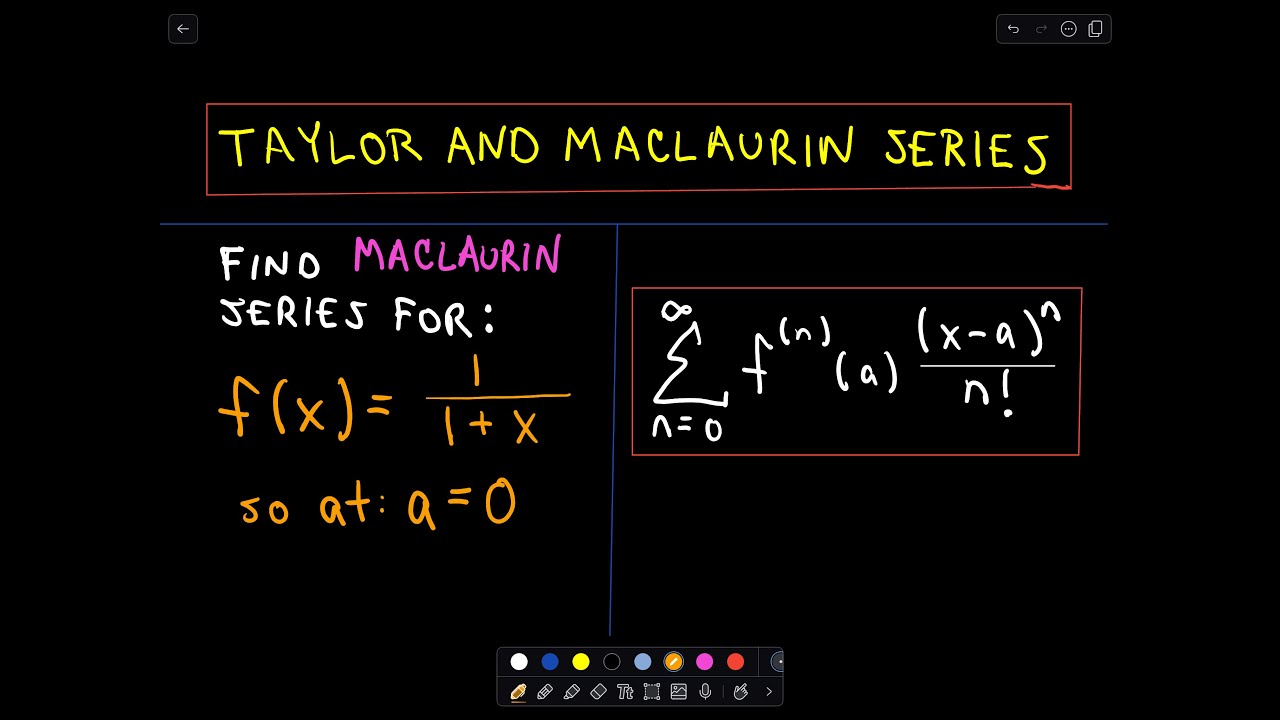
Finding A Maclaurin Series Expansion Another Example 1 Youtube

Upon Deriving Maclaurin S Series Expansion Of Tan X The Coefficients Are 1 16 272 7 936 37 594 What S The Pattern Among These Numbers Quora

Solved An Helpful Info Power Series Expansion For Logari Chegg Com

Expansion Of Log 1 X And Log 1 X Maclaurin Series 7 Youtube

Taylor Series Wikipedia
Solved Using The Power Series Expansion Course Hero

Solved An Helpful Info Power Series Expansion For Logari Chegg Com



