Log1+x Power Series
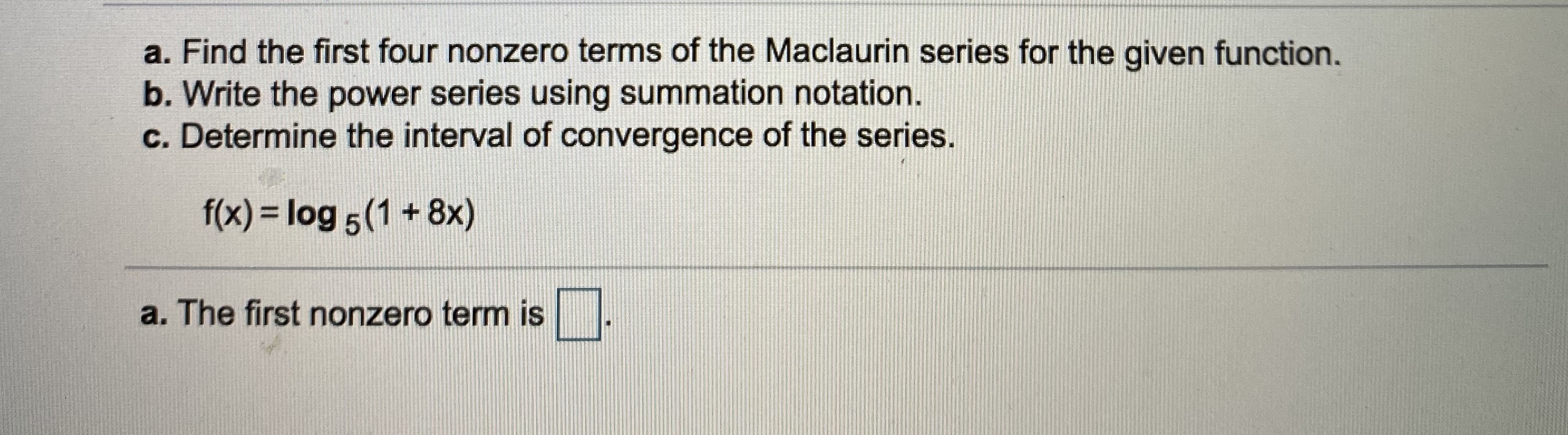
Answered A Find The First Four Nonzero Terms Of Bartleby
2

Taylor Series Wikipedia
Http Www Maths Usyd Edu Au Math2962 R Pdf Tut08s Pdf
Http Citeseerx Ist Psu Edu Viewdoc Download Doi 10 1 1 22 3145 Rep Rep1 Type Pdf
A Differentiate The Taylor Series About 0 For The Following Functions B Identify The Function Represented By The Differentiated Series C Give The Interval Of Convergence Of The Power Series For The
A power series about a, or just power series, is any series that can be written in the form, \\sum\limits_{n = 0}^\infty {{c_n}{{\left( {x - a} \right)}^n}} \ where \(a\) and \({c_n}\) are numbers.

Log1+x power series. HOWEVER, we must do more work to check the convergence at the end. What is the binomial expansion for (1+x)^-1?. Parentheses are sometimes added for clarity, giving ln(x), log e (x), or log(x).
Power series The Logarithm Radius of convergence Boundary behaviour Summation by parts Back to the boundary Radius of convergence Theorem Given a power series P n a n(z −z 0)n there is an R such that P n a n(z −z 0)n converges if |z −z 0| < R P n a n(z −z 0)n diverges if |z −z 0| > R In addition:. An expansion for log e (1 + x) as a series of powers of x which is valid only, when |x|<1. The \({c_n}\)’s are often called the coefficients of the series.
Ez = X∞ n=0 zn n!, where z is any complex number. The radius of convergence stays the same when we integrate or differentiate a power series. Multivariate Taylor series is used in many optimization techniques.
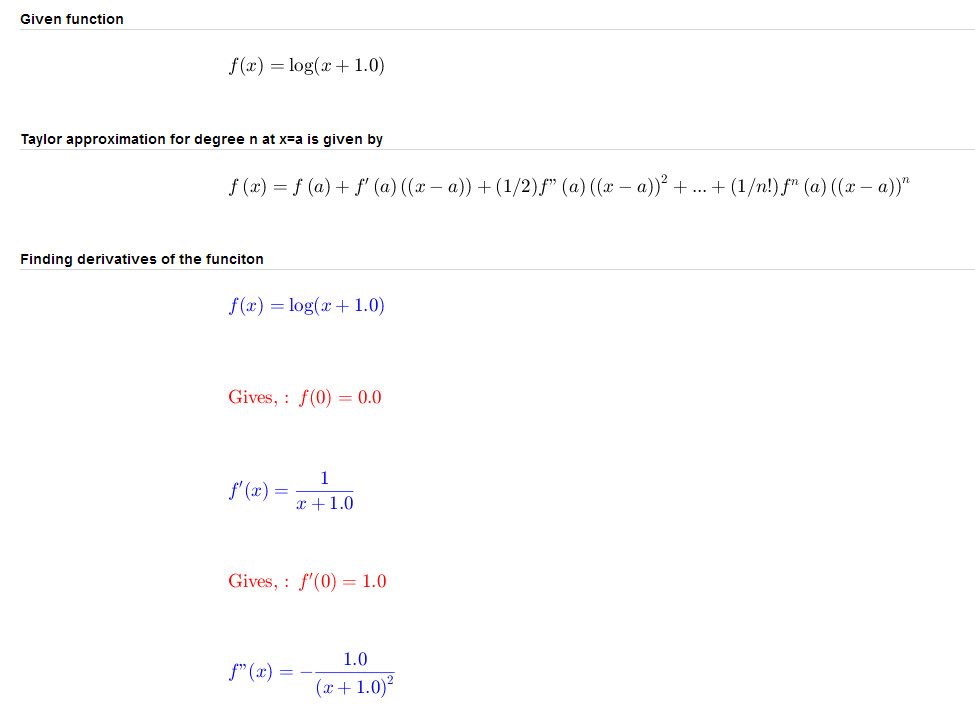
Taylor series If a function \(f\left( x \right)\) has continuous derivatives up to \(\left( {n + 1} \right)\)th order inclusive, then this function can be expanded in a power series about the point \(x = a\) by the Taylor formula:. Taylor series expansions of logarithmic functions and the combinations of logarithmic functions and trigonometric, inverse trigonometric, hyperbolic, and inverse hyperbolic functions. To find the power series for ln(1 - x) we.
To find the Radius of Convergence of a power series, we need to use the ratio test or the root. The interval of convergence is the open, closed, or semiclosed range of values of x x x for which the Maclaurin series converges to the value of the function;. Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals.
The function f(x) = 8 x ln (1 + x) is represented as a power series:. If r < R then the series converges. As stated on the title, my question is:.
As you can see ln1 = 0. Get the free "Log(1-x) Taylor Series" widget for your website, blog, Wordpress, Blogger, or iGoogle. Whether the series converges or diverges, and the value it converges to, depend on the chosen x-value, which makes power series a function.
Log1p(x) is more accurate than log(1+x) for small values of x. For small x, log1p(x) is approximately x, whereas log(1+x) can be zero. This series is used in the power flow analysis of electrical power systems.
Radiation lifetime in a cavity Index. The natural logarithm of a number is its logarithm to the base of the mathematical constant e, where e is an irrational and transcendental number approximately equal to 2.718 281 8 459.The natural logarithm of x is generally written as ln x, log e x, or sometimes, if the base e is implicit, simply log x. Y = log1p(x) computes log(1+x), compensating for the roundoff in 1+x.
Find a power series representation for tan−1 x. Power series expansion for logarithmic terms:. Show that log (1+x) = x - x 2 \2 + x 3 \3.
The geometric series is a simplified form of a larger set of series called the power series. Find more Mathematics widgets in Wolfram|Alpha. Every power series has an interval of convergence - although in some cases it is all real numbers or just a single number.
(−),where f (n) (a) denotes the n th derivative of f evaluated at the point a. Tall Arrays Calculate with arrays that have more rows than fit in memory. Hence for m > A, m i I) -(e2ri/m _ l)n < m A A 2-eO as me x).
F(x) = e x. Power Series Representation for ln(1+x). Deriving the Maclaurin expansion series for ln(1+x) is very easy, as you just need to find the derivatives and plug them into the general formula.
Expansions at generic point z==z 0. Some Important results from logarithmic series (2) The series expansion of log e (1 + x) may fail to be valid, if |x| is not. We know Z 1 1 + x dx = ln(1 + x).
By using this website, you agree to our Cookie Policy. We have 1 (1−x)2 d dx 1 1−x and 1 1−x X∞ n=0 xn, hence 1 (1−x)2 d dx X∞ n=0 x n= X∞ n=0 d dx xn = X∞ n=1 nx −1 = 1+2x+3x2 +4x3 +··· = X∞ n=0 (n+1)xn (re-indexed)The radius of convergence is R = 1. For example, we can use them to define transcendental functions such as the exponential and trigonometric functions (and many other less familiar functions).
Categories General s Power series solution for Log(1+x) Leave a Reply Cancel reply. C_2 = c_3 = c_4 = c_5 = c_6 = Fi. That function is the antiderivative of 1/(1+x2.
In a power series, the coefficients may be …. The Taylor series of a real or complex-valued function f (x) that is infinitely differentiable at a real or complex number a is the power series + ′ ()!(−) + ″ ()!(−) + ‴ ()!(−) + ⋯,where n!. From (1) we find m(e2ftIlm-1) - 27ri as m -e , so that Ie2ffi/m < A m where A is a constant independent of m.
Denotes the factorial of n.In the more compact sigma notation, this can be written as ∑ = ∞ ()!. The radius of convergence is half the length of the interval;. However, use of this formula does quickly illustrate how functions can be represented as a power series.
We use the polynomial with infinitely many terms in the form of power series. Actually, just to give ourselves some closure here, let's write it in sigma notation. -1)"+1 log(1+x)= Question # 2 (25 pts.):.
Given translated logarithmic function is the infinitely differentiable function defined for all - 1 < x < oo. Power series is a sum of terms of the general form aₙ(x-a)ⁿ. F(x) = sum_{n = 0}^{infty} c_n x^n.
Usually, a given power series will converge (that is, approach a finite sum) for all values of x within a certain interval around zero—in particular, whenever the absolute value of x is less than some positive number r, known as the radius. Power Series Power series are one of the most useful type of series in analysis. (a) represent the function $ f(x) = 1/x $ as a power series around $ x = 1 $.
For the function itself. The power series a n x n converges absolutely at every point x from the open interval -r < x < r and diverges for all x outside this interval. Previous Post Previous How do you write:.
ON THE POWER SERIES FOR LOG (1 + Z). Applications of Natural Log Series. Introduction A power series (centered at 0) is a series of the form ∑∞ n=0 anx n = a 0 +a1x+a2x 2.
1 1 + x = 1 1 ( x) = X1 n=0 ( x)n = X1 n=0 ( n1) xn Now let’s integrate back 290. Series Expansion of Exponential and Logarithmic Functions. Your email address will not be published.
Each term is a power of x multiplied by a coefficient. A power series does not necessarily represent the function for all values of x. So we gure out the power series representation for 1 1 + x and integrate it to get ln(1 + x).
73 K is independent of m, and may therefore be evaluated by letting m tend to infinity. So, the function 1/(1-x) can be represented as a power series for part of its domain.In similar ways, other functions can be represented by power series. In the process we underwent to find his series, one of the steps included.
Using this power series definition, one can verify that:. Consider the function of the form \f\left( x \right). Find a power series representation for ln(1 + x) and it’s radius of conver-gence.
Problems on Taylor’s Theorem. > series( 1/(1-x), x = 3, 12);. Note *Power Series are in the form:.
Expansion of log e (1 + x) if |x|<1 then Replacing x by −x in the logarithmic series, we get. Free Taylor/Maclaurin Series calculator - Find the Taylor/Maclaurin series representation of functions step-by-step This website uses cookies to ensure you get the best experience. If you're seeing this message, it means we're having trouble loading external resources on our website.
Functions as Power Series. For example, only for | x | < 1. A power series is any series of the following form:.
Exponential Function:The function which is in the form of $$\;y=f(x)=a^x,\;\;\;\;\;a>0$$ is called an exponential function in which the base a is constant and the power or index x is a variable. At the endpoints - r and r , the series may converge or diverge so, these points must be checked for convergence, individually. In this section we discuss how the formula for a convergent Geometric Series can be used to represent some functions as power series.
Once you differentiate, you end up with a simple reciprocal. ∑ n = 0 ∞ c n (x − a) n \sum_{n=0}^{\infty}c_n(x-a)^n ∑ n = 0 ∞ c n (x − a) n where c n c_n c n are the coefficients of each term in the series and a a a is number. To use the Geometric Series formula, the function must be able to be put into a specific form, which is often impossible.
We begin with the complex exponential function, which is defined via its power series:. Series expansions of exponential and some logarithms functions. Finding the Power Series for ln(1 - x) A power series is the sum of an infinite number of terms.
Next Post Next Prove that A – (B U C) = (A – B) ∩ (A – C) Search for:. Expansion of logarithmic series. Power series, in mathematics, an infinite series that can be thought of as a polynomial with an infinite number of terms, such as 1 + x + x 2 + x 3 +⋯.
Differentiating it again simply increases the power as you can see. Consider the function of the form \f\left( x \right) = \sqrt {1 + x} \. Exponential and Logarithmic Function and Series,Expansion of e^x,a^x and log(1+x) xx.
(b) represent the function $ f(x) = \ln (x) $ as a power series around $ x = 1 $. Students, teachers, parents, and everyone can find solutions to their math problems instantly. A power series $\displaystyle\sum_{n=0}^\infty c_n x^n$ can be thought of as a function of $x$ whose domain is the interval of convergence.
In a geometric series, every term has the same coefficient. You may remember from geometric series that for appropriate values of r.Similarly, this tells us from a power series perspective that when x is between -1 and 1. X1n = 0.3" un x2n = an -0.3 an-1 and x3n is obtained by convolving xin and x2n that is x3n = x1n * x2n * x2n a) Find the complex cepstrum, î;(n).
In this tutorial we shall derive the series expansion of the trigonometric function $${a^x}$$ by using Maclaurin's series expansion function. E z1+ 2 = ez1ez2, for all complex z 1 and z 2. The first thing to notice about a power series is that it is a function of \(x\).
\dfrac {1} {1+x}=1-x+x^2-x^3+\ldots\quad (|x|<1) and take into account that all power series can be integrated term by term on an interval lying inside the interval of convergence. Notice how the power series differs from the geometric series:. Natural log of one plus x to the third power is x to the third power minus x to the sixth over two plus x to the ninth over three, so on and on and on.
It is also the radius of the circle in the complex plane within which the. In this tutorial we shall derive the series expansion of $$\sqrt {1 + x} $$ by using Maclaurin's series expansion function. Five times the sum of a number and one?.
The sum of partial series can be used as an approximation of the whole series. Determine the Taylor series at x=0 for f(x) = e x. Outside the domain, the Maclaurin series either is undefined or does not relate to the function.
The power series expansion of the logarithmic function Let represent the translated (shifted) logarithmic function f (x) = ln (x + 1) by the power series. Free math lessons and math homework help from basic math to algebra, geometry and beyond. For math, science, nutrition, history.

Solved An Helpful Info Power Series Expansion For Logari Chegg Com
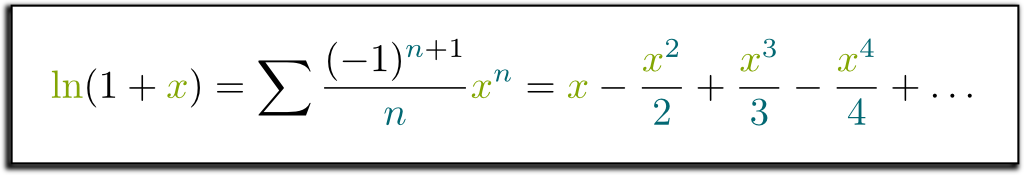
Logarithms And Age Counting Science4all

Taylor Series Wikipedia
2

Find The Power Series Representation For F X 3 X Be Detailed In Steps Please Homeworklib
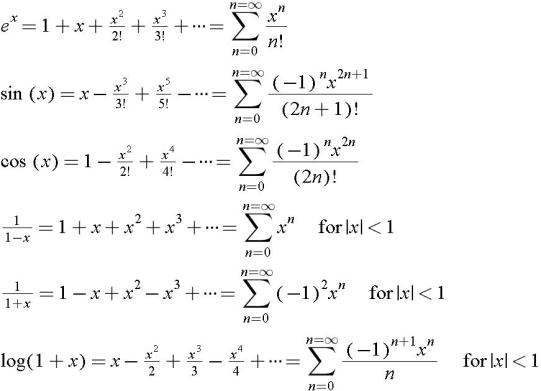
Appendix C Expansions Differentiation Integrals And Mathematical Relations Engineering360
3

Natural Logarithm Wikipedia
How To Expand Log 1 Log 1 X In Powers Of X As Far As X 4 Quora

Solved 1 A 5 Pts Expand 1 X2 In A Power Series Wit Chegg Com
2
Solved Using The Power Series Expansion Course Hero
2
Projecteuclid Org Download Pdf 1 Euclid Tjm

Solved 1 Determine The Radius Of Convergence And Interva Chegg Com

Solved An Helpful Info Power Series Expansion For Logari Chegg Com

Class Notes 9 Power Series 1 3 Ppt Download

Solved Find The Radius Of Convergence For The Following P Chegg Com
Http Citeseerx Ist Psu Edu Viewdoc Download Doi 10 1 1 493 2397 Rep Rep1 Type Pdf
2

Power Series
Www Maths Ox Ac Uk System Files Legacy W8 Trudgian Pdf

Taylor Series For F X Ln X Centered At X 1 Youtube
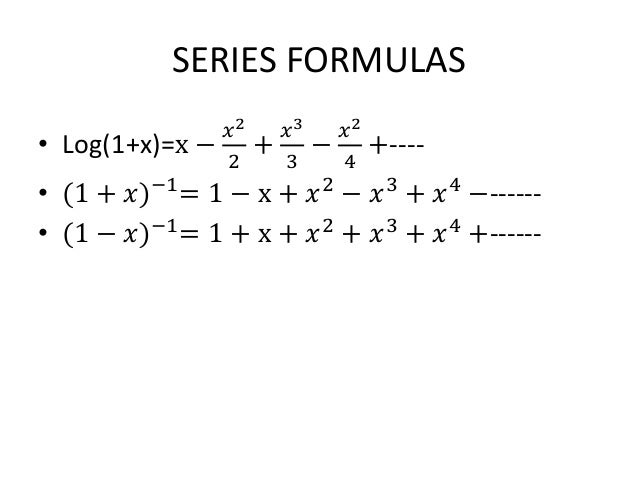
Power Series

Chapter 10 Infinite Series Ppt Download
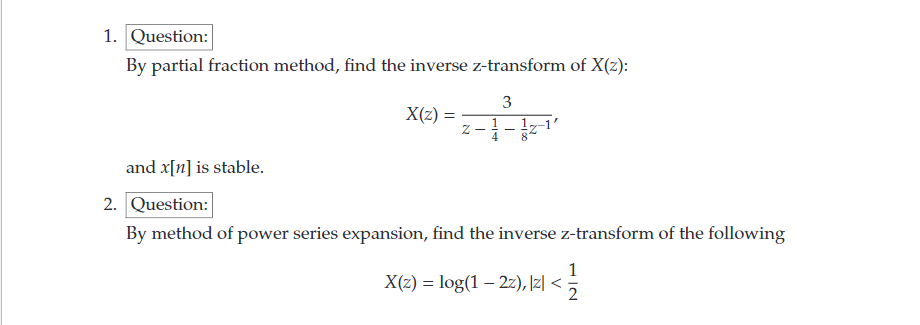
Solved 1 Question By Partial Fraction Method Find The I Chegg Com

8 Prove That Dt 1 T N 1 For X E A A 0 A 1 And Deduce From There A Power Series Expansion For In 1 X 8 Prove That Dt 1 T N 1 For X E A A 0 Homeworklib

Solved Plese Answer B And C I Send The Final Result Chegg Com
137 1 49 7 Course Builder 1617 Math1010c Exp and log Pdf

Taylor Series Wikipedia

Solved Find The Following Limit Lim X Rightarrow 0 Ln 1 Chegg Com

Solved A 5 Pts Expand 1 X2 In A Power Series With Ce Chegg Com

Natural Logarithm Wikipedia
Projecteuclid Org Download Pdfview 1 Euclid Aop

Power Series Representation Of Functions Calculus 2 Youtube

Solved 5 Pts What Is The Power Series For Log 1 4x Chegg Com
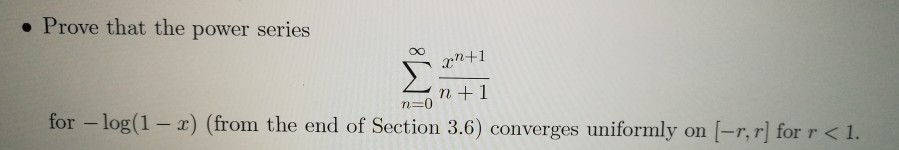
Solved Prove That The Power Series N 1 For Log 1 2 Chegg Com
Projecteuclid Org Download Pdf 1 Euclid Facm

Power Series Taylor S And Maclaurin S Series
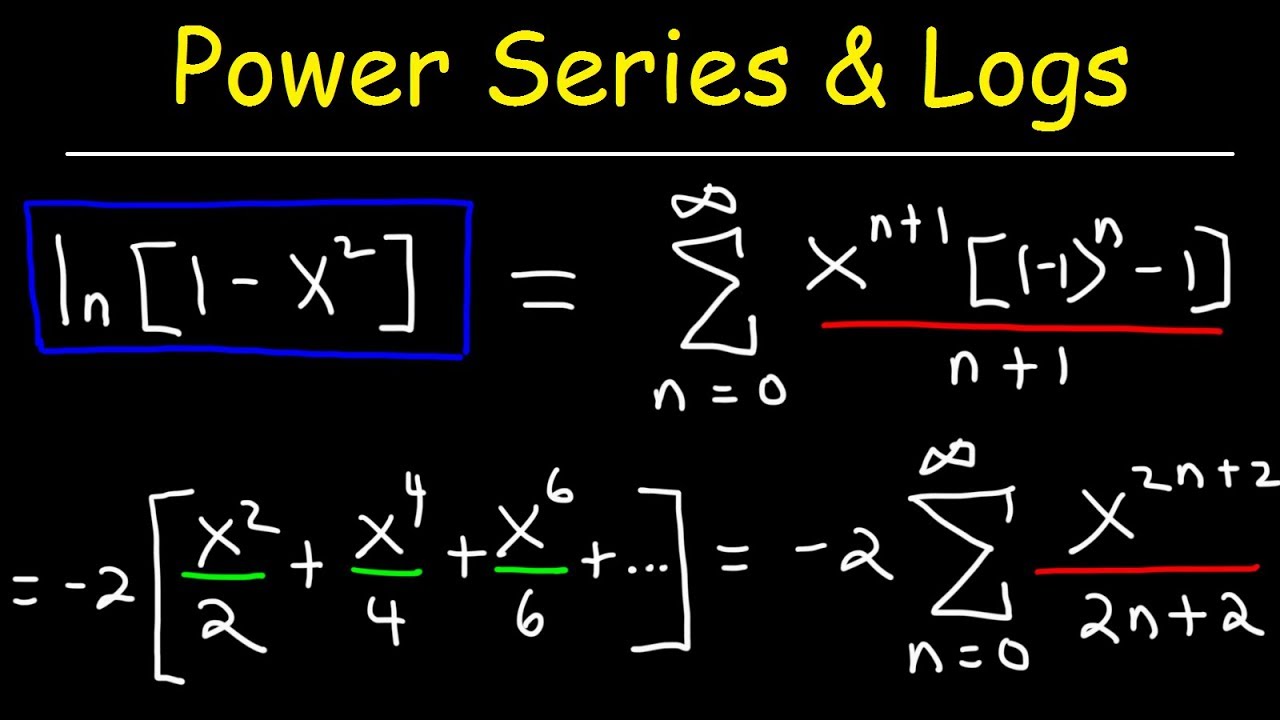
Power Series Representation With Natural Logarithms Calculus 2 Youtube
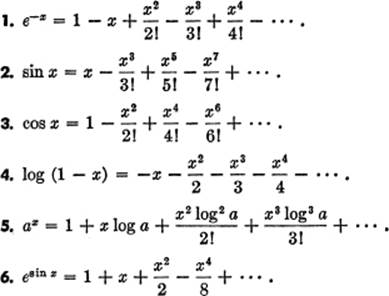
Expansion Of Functions Expansion Of Functions The Calculus Primer
Expand Log X In Powers Of X 1 By Taylor S Series Sarthaks Econnect Largest Online Education Community

Expansion Of Log 1 X Maclaurin Series Youtube

Taylor Series Wikipedia

Chapter Vi

Power Series Taylor S And Maclaurin S Series
Q Tbn 3aand9gctsgw9vft4mnh Bijnjv0lau9ncbgfjor ujy9dpdwsb5rxwi Usqp Cau

Taylor Series For F X Ln X Centered At X 1 Youtube
2

Taylor Series Wikipedia
Taylor Series
Www Mdpi Com 2571 905x 2 1 2 Pdf

Representing The Ln 1 X Power Series How To Steps Study Com
How To Expand Log 1 Log 1 X In Powers Of X As Far As X 4 Quora
2

Power Series Expansion Of Log X Power Series In Bengali Youtube

Taylor Series Wikipedia

Pdf A New Zero Test For Formal Power Series
Q Tbn 3aand9gcskxb6gvgapdft5ibnrins2t92z0suwezny Nudtzbvqw8wmwu8 Usqp Cau
What Is The Expansion Of Log 1 X Quora
2

2 Question By Method Of Power Series Expansion Chegg Com
Arxiv Org Pdf 1903

X 5 2 Log 國立台灣科技大學
How To Expand Log 1 Log 1 X In Powers Of X As Far As X 4 Quora

Solved 1 Find The Power Series Expansion Of F X Z Chegg Com
Http Archive Ymsc Tsinghua Edu Cn Pacm Download 81 8733 Dlogalgsubmit Pdf
Search Q Logarithm Expansion Of Log X Tbm Isch

Natural Logarithm Wikipedia

Expand Logex In Power Of X And Hence Evaluate Loge 1 1 Correct To Four Decimal Places Answer Mathematics 1 Question Answer Collection

Ppt Section 9 8 And 9 9 Power Series Powerpoint Presentation Free Download Id

Power Series Of Ln 1 X Video Khan Academy

Taylor Series Wikipedia

Representing The Ln 1 X Power Series How To Steps Study Com

Pdf Sums Of Series Involving Central Binomial Coefficients Harmonic Numbers

Cauchy Euler Equation Power Series Collegexam
Www Worldscientific Com Doi Pdf 10 1142 0017
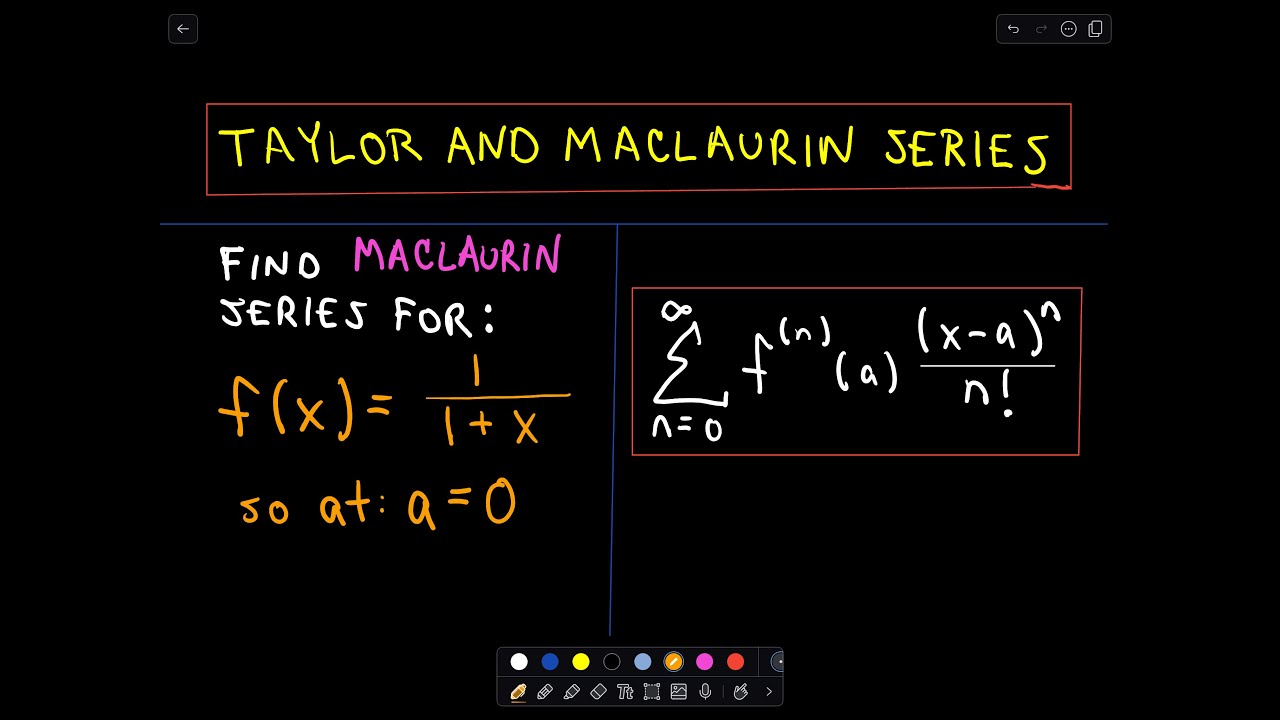
Finding A Maclaurin Series Expansion Another Example 1 Youtube
Http People Math Sc Edu Girardi M142 Handouts 10staylorpolyseries Pdf

Natural Logarithm Wikipedia
Http Www Sfu Ca Mdevos Notes Comb Struct Genfunct Pdf

Analysis Webnotes Chapter 07 Class 46

Worksheet Practice Problems Power Series Of Ln Functions Study Com

Pdf Generalized Extended Weibull Power Series Family Of Distributions Semantic Scholar

Solved Suppose That Sigma N 0 Infinityconverges Show T Chegg Com

Representing The Ln 1 X Power Series How To Steps Study Com

Taylor Series

Power Series Taylor S And Maclaurin S Series
Http Bsmath Hu P Erdos 1954 01 Pdf

Taylor Series Wikipedia
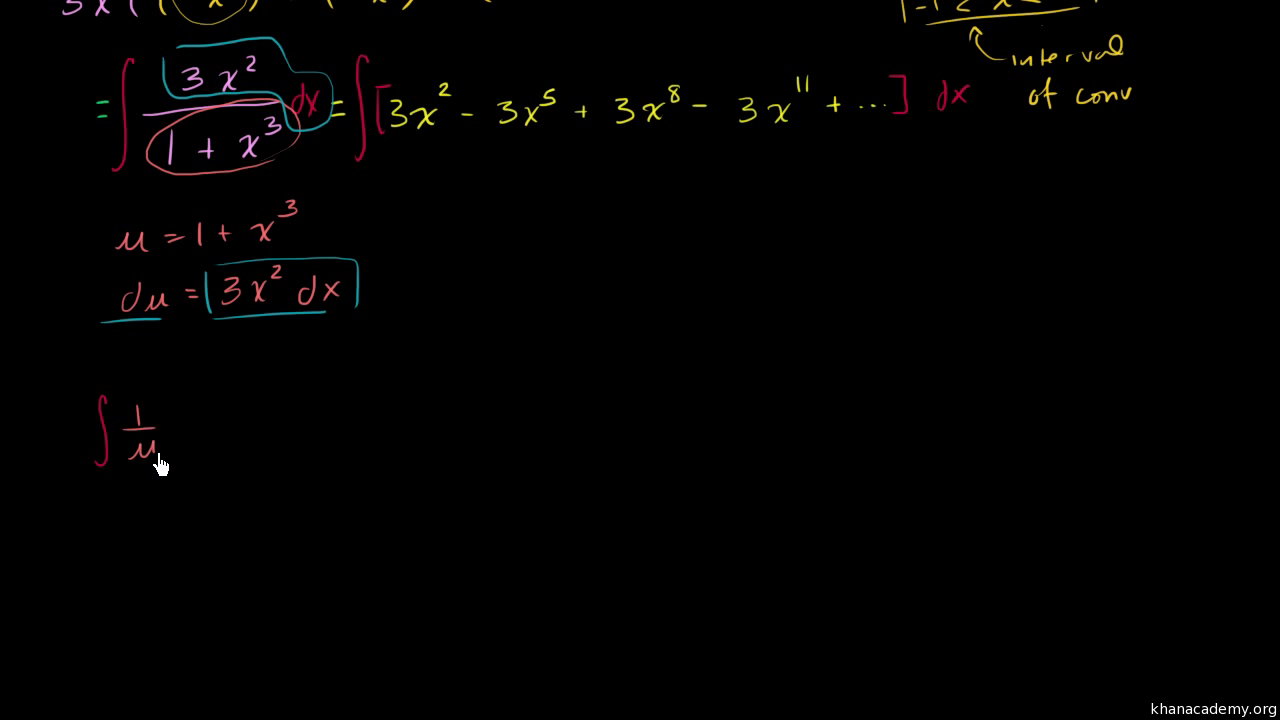
Power Series Of Ln 1 X Video Khan Academy

Power Series Involving Natural Logarithm Ln 1 X 1 X Youtube

Dc Response Discrete Time Fourier Transform X N X Ejw Ppt Download

Chapter 10 Infinite Series Early Results Power Series An Interpolation On Interpolation Summation Of Series Fractional Power Series Generating Functions Ppt Download
2

R60rln22bih8dm

Taylor Series Wikipedia

Video 2737 Power Series Representation Of Ln 1 X Part 2 2 Youtube



