X2+y2 偏微分

Nmt Tutorial 3扩展b 自动微分 Tingxun S Blog

身勝手な主張 187ページ目
Cantor Math Ntnu Edu Tw Wp Content Uploads 09 E6 Ad E5 B9 B4 E5 81 8f E5 Be Ae E5 86 E6 96 B9 E7 A8 8b Pdf
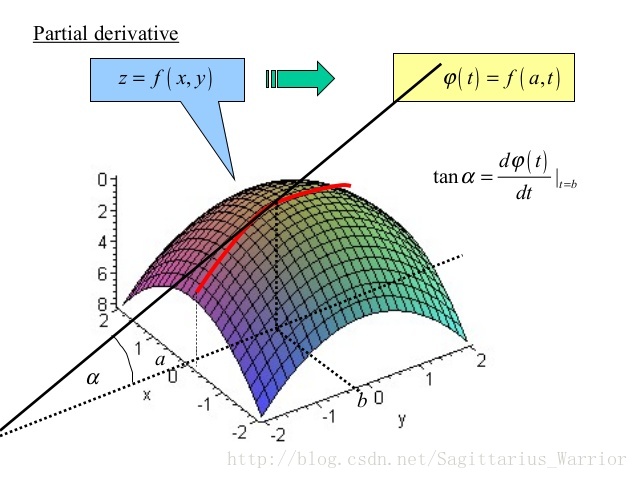
用python学 微积分b 多元函数的微分 Sagittarius Warrior的博客 Csdn博客 Python多元函数积分
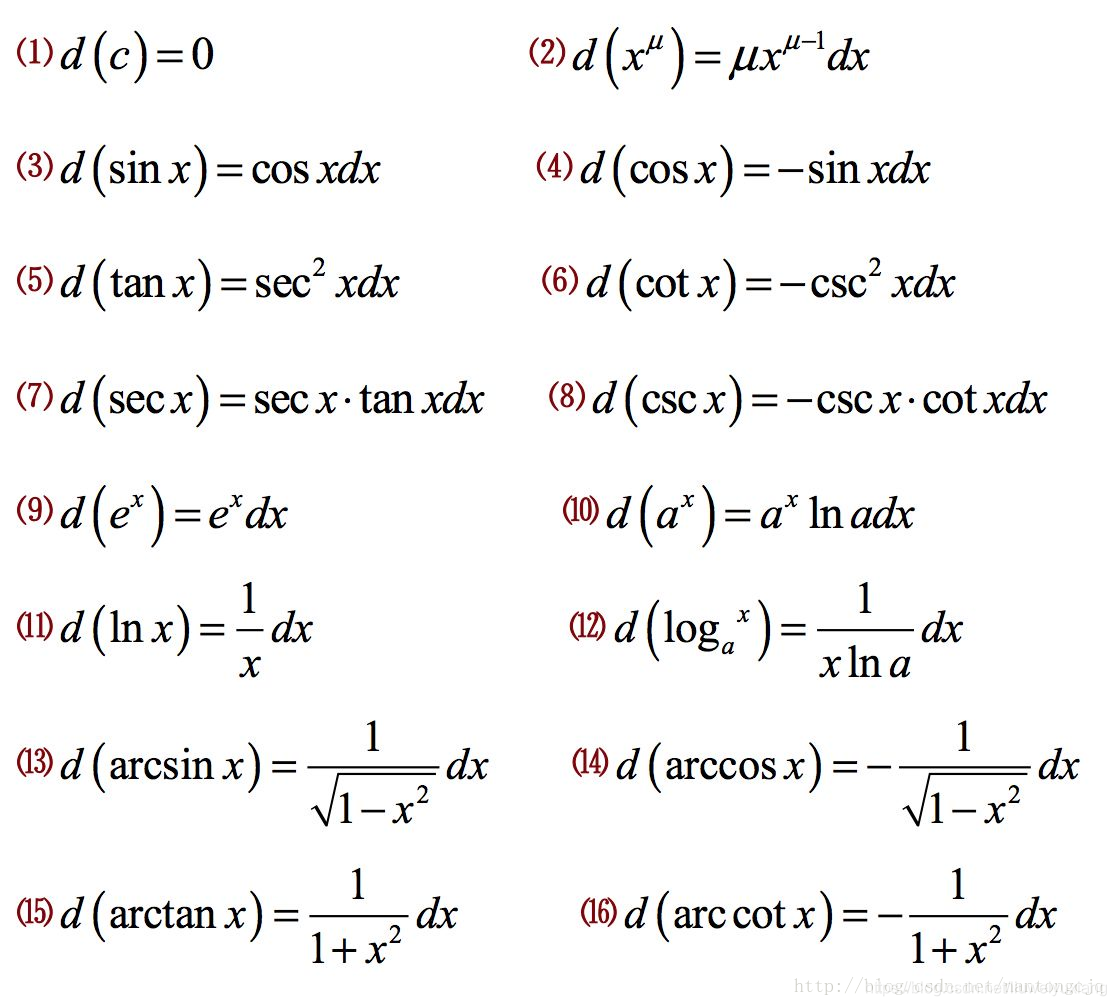
微分和积分公式大全 Lavi的专栏 Csdn博客 积分公式

一些偏微分方程的筆記
12 合成関数の微分 12.1 f(x(t),y(t)) の微分 定義12.1 関数f(x,y) がC1-級であるとは,偏導関数fx,fy が存在し て,しかも連続である時に言う. 定理12.1 (教科書p.180, 定理5.5) z = f(x,y) がC1-級で,x = x(t),y = y(t) がt について微分可能なら ば,z = f(x(t),y(t)) もt について微分可能で, dz dt = fx(x(t),y(t))_x(t)+fy(x(t),y.

X2+y2 偏微分. (1)f(x,y)=exy とします.f(x,y)のx 方向の偏導関数はy を定数と見てx についての1 変数関数と思って微分しますから. F は任意関数であるから, 条件が無いと決められない. そこで例えばu(x;y) = sinx on fy = 0gとしてみよう. 多変数関数と偏導関数 二変数関数f(x,y) について各点(x,y) において偏微分係数 を考えることによって決まる二変数関数 ∂f ∂x (x,y), ∂f ∂y (x,y) をf(x,y) のx 又はy による偏導関数とよぶ。 fx(x,y),fy(x,y) とも書く。 三変数以上の多変数関数 についても同様に偏.
つまり、 : で偏微分したときの における値 : で偏微分したときの における値 を表します。 例題2 \ f(x,y) = 9x^2 - 6xy + 4y^2 \の偏導関数と点 における偏微分係数を求めなさい。. 第2 節『偏微分係数・偏導関数』 3 演習問題No.2 担当:新國裕昭 1.2 偏微分係数・偏導関数 教科書p.115~p. 2つの独立変数 \( x \), \( y \) を持つ関数 \( z=f(x, y) \) について, 変数 \( y \) を変化させることなく固定して変数 \( x \) だけについて \( f \) を微分することを, \( f \) の \( x \) に関する偏微分という.
Fの(a,b) でのyに関する偏微分係数と呼ぶ.すなわち, ∂f ∂y (a,b) = lim k→0 f(a,b+k)−f(a,b) k. §5.偏微分 • f(x,y) が(x,y) = (a,b) で偏微分可能⇐de⇒f 函数x 7→ f(x,b) が微分可能. その微分係数をxに関する偏微分係数と呼び,f x(a,b), ∂f ∂x (a,b) と表す:∂f ∂x (a,b) = limx→a f(x,b)−f(a,b) x−a 領域D の各点でf(x,y) がxに関して偏微分可能であるとき,函数D 3 (x,y) 7→ f x(x,y)を,f(x,y)のxに関する. 偏微分と全微分 Jacques Garrigue, 08年10月15・22日 偏微分 関数x 7!f(x,b) がa で微分可能なら,f(x,y) が(a,b) でx に関して偏微分可能だと いう. 偏微分係数は fx(a,b) = ∂f ∂x (a,b) = limx!a f(x,b)¡f(a,b) x¡a f が開領域D の各点でx に対して偏微分可能なら,z = f(x,y) のx に関する偏導関数が定義.
(2) f(x,y)=logx y,(x > 0,x 6=1 ,y > 0). 117 の問6, 7, 8,例題3, 問9 を解いた上で,さらに以下の問題に答えよ. 偏微分とは、n 変数関数 f(x 1, x 2, …, x n) のある一つの変数 x i 以外の n-1 個の変数の値を固定することで、f を x i だけの関数とみて、この関数を x i について微分することです。.
偏微分 多変数の関数 w=f(x, y, z, ) について,1つの変数だけを変化させ,他の変数は定数と見なして,微分したものを偏微分(偏導関数)といい,. (そもそも偏微分なのだろうか?) 具体例で考えます。 f(x,y) = (x+2y)^2 g(x,y) = x+2y である場合。当然∂f/∂g = 2 gです。このような場合は問題ありませんが、 f(x,y) = x + 3y g(x,y) = x + 2y のような場合はどのように考えたらよいのでしょうか? 全微分の関係を使って. 微分積分学I 演習問題8 3 停留点(0;1) において, ヘッセ行列式 xx f fxy fyx fyy 4 0 0 2 = 8 < 0 なので, この点は極小でも極大でもない.
そして, 関数 \( z=f(x, y) \) 上の点 \( \left(a, b\right) \) の周囲が十分に. 偏微分y を定数と考えてxで微分する.y = bとおいて,1 変数xの関 数f(x,b)を考える.f(x,b)をxで微分するlim h→0 f(a+h,b) −f(a,b) h これが 定義されるとき,f(x,y)は(x,y)=(a,b)でxについて偏微分可能であると いい,その値をf(x,y) の(x,y)=(a,b) でのx に関する偏微分係数と. 偏微分可能性と偏微分係数 Definition (偏微分係数)点(a, b) の近傍で定義された関数f(x, y) に対して,極限 lim h→0 f(a + h, b) − f(a, b) h が収束するとき,f(x, y) は点(a, b) でx に関して偏微分可能であるとい う.このとき ∂f ∂x (a, b) = limh→0 f(a + h, b) − f(a, b) h (= fx(a, b)) とおき,点(a, b) におけるf(x, y.
1 偏微分法 17年9月27日小テスト解答 I偏導関数f x とf y を計算しましょう. (1)f(x;y) = 1 x2+y2 (2)f(x;y) = (x+4y)(2x+y) 解答(1) f x = 2x x2 +y2;. 1 第5章 偏微分 5.1 2変数関数 Dをxy平面の部分集合とする.Dに含まれる各点(x;y)に対して実数z= f(x;y)が対応し ているとき,fをDを定義域とする(2変数)関数という.また,(x;y;z)を空間内にプロットし たものをfのグラフという. R上の関数のグラフが曲線になるように,2変数関数のグラフは曲面に. 例えば,関数 \(f(x,\ y) = x^2 - y^2\) について \(x\) で偏微分すると \(f_x(x,\ y) = 2x\).
−2 − 10 年度「数学5」 < 2変数関数> 例1 °1 縦xcm,横ycm の長方形の面積をzcm2 とすると,z = xy である。 °2 底面が半径xcm の円で、高さがycm の円柱の体積をzcm3 とすると,z = πx2y である。 一般に3 つの変数x,y,z があり,x,y のおのおのの値の組に対して、z の値がただ1 つ定まるとき,. 熊本大学数理科学総合教育センター x2 偏微分の定義と基本性質 演習問題1 ˇ 問題の難易度の目安基礎9 標準8 発展8 1(9)(偏微分の定義) 次の空欄に適切な数式を入れよ. f(x;y) を2変数関数とする.f(x;y) が点(a;b) でx に関して偏微分可能であるとは,極限値. 数学の多変数微分積分学における偏微分(へんびぶん、 partial derivative )は、多変数関数に対して一つの変数のみに関する(それ以外の変数は 定数として固定する (英語版) )微分である(全微分では全ての変数を動かしたままにするのと対照的である)。 偏微分はベクトル解析や微分幾何学.
微分すると,0になり,x2 をx で偏微分するのは普通の微分と同じだか ら,2 x となる.したがって,結果として, @ ( x 2 −y 2 ). 偏微分係数の定義から分かるように,偏導関数は,一方の変数を定数とみなして微分すれば求められます。なお,偏導関数を求めることを 偏微分する といいます。 例題2-1. 解説2 \ f_x = 18x - 6y , \ \ f_y = -6x + 8y \となる。.
例題と演習で学ぶ 微分積分学 演習問題解答 (第6刷にも対応) 第3章 3.1. 2変数関数 z=f(x,y) に対し、各変数方向への偏微分と無限小の積をすべての変数について加えたものを zの全微分といいます。2変数関数 z=f(x,y) の全微分は df=∂f/∂x dx+\∂f/∂y dyと表すことができる。. ちなみに,呼び方は例えば,∂f ∂x はラウンドfラウンドxと呼ぶ. f がDの各点でxに関して偏微分可能なとき,f はDでxに関し て偏微分可能であるといい,各点に対応.
微積分II 14 春学期 8 3 偏微分と2 変数関数の微分式 微積分I では独立変数がひとつしかない関数, これを1 変数関数という, を 扱ってきたが, 微積分II では独立変数がふたつの関数, 2 変数関数, の微分を 考察する.具体的には, 普通は2 つの独立変数をx とy で表し, それに従属す. 同次形微分方程式は、u = y/x と置換することで変数分離型になります。 こんなことは、相当チャラい参考書にも、ネットの勉強サイトにすら書いてある。 dy/dx = 2xy/(x^2+y^2) を u = y/x で変換すると、 (du/dx)x + u・1 = 2u/(1+u^2). X^2 + y^2 = 4 \のように 明示的( の形)に , の関係が示されていないもの を表します*1。 2.陰関数定理(陰関数の導関数の求め方) 偏微分を用いると陰関数表記であったとしても導関数 を簡単に求めることができます。.
(連続性) 次の関数f(x;y)の原点における連続性を調べる。上に示した「色々な 近づき方」のそれぞれについて、f(x;y) がf(0;0) に近づいているか調べよ。その上で、. Y^2をxについて微分してくださいdy^2/dx = (dy^2/dy)(dy/dx) = (2y)(dy/dx) です。この式から y を消すためには、y を x で表す式をどこからか持ってこないとなりません。. 2.3 高階の偏微分 関数f(x;y) の偏導関数fx = @f @x やfy = @f @y が再びx やy について偏微分可 能ならば、さらにその偏微分fxx = @ 2f @x2, fxy = @ f @y@x, fyx = @2f @x@y, fyy = @2f @y2 などを 考える事ができる。ここで、fxy = (fx)y の意味で,x で偏微分した後にy で偏微 分する事を表す。.
F y = 4 (2x+y)+(x+4y) 1 = 9x+8y II関数 f(x;y) := x2 +xy +y2 4x 6y の停留点を求めましょう. 解答 f x = 2x+y +0 4 0 = 2x+y 4 = 0 f y = 0+x 1+2y 0 6. 2 次偏導関数の性質 2 次偏導関数に関する重要な性質は次のものである. Theorem f(x,y) を領域D で定義された関数とする.2次偏導関数fxy とfyx が存 在し,さらにfxy とfyx がともにD で連続ならば,D 上で fxy(x,y) = fyx(x,y) が成り立つ.つまり,偏微分の結果は変数の順番によらない.. F y = 2y x2 +y2 (2) f x = 1 (2x+y)+(x+4y) 1 = 4x+9y;.
熊本大学数理科学総合教育センター x2 偏微分の定義と基本性質 演習問題1 解答 ˇ 問題の難易度の目安基礎9 標準8 発展8 1(9)(偏微分の定義) 次の空欄に適切な数式を入れよ. f(x;y) を2変数関数とする.f(x;y) が点(a;b) でx に関して偏微分可能であるとは,. 今回は数学Ⅲで学習する微分法の単元から 『対数(log)の微分』 について解説していきます。 対…. (1) lim (x;y)!( 1;2) (2x+y) = 2( 1)+2 = 0.
関数f の定義域の各点(x,y) に対して偏微分係数fx(x,y),fy(x,y) の値を対応させる2 変数関数を,それぞれx,y に関する偏導関数と呼ぶ.やはり,fx(x,y),fy(x,y), ∂f ∂x (x,y) などと書く.偏導関数を求めることを,偏微分するという.前回の例題を再録する. 例題1.2. 方向微分の際,(1,0) を方向として取ると,点(x0,y0) における方向微分係数は lim h→0 f(x0 +h,y0)−f(x0,y0) h となる.この極限が存在するとき,関数f(x,y)は点(x0,y0)においてx で偏微分可能であるという. その極限値をxについての偏微分係数という.f(x,y)の定義域上のすべてのxで偏微分係数が存在. すると, u(x;0) = 0+f(x+02) = sinx となり, f(x) = sinx となる.
(3) f(x,y)=tan−1 y x,(x 6=0). 合成関数の微分への利用 3 後のy,z についての偏微分についても同じ方法でもとまります.結果だけ書いておくと ∂r ∂y = y r (11) ∂r ∂y = y r (12) です.こうして(9) , (11) , (12) から(1) が得られる事が示されました. 補足説明 ここでは与えた式(4) の導出を説明しておきます.実はこの式は,全微分.
Cosine裡面可以放 1 向量分析大典 偏導數partial Derivative

五点微分 Ln微分 微分公式 微分计算

U X Y Log X 2 Y 2 1 写真に示すように偏導関数 U Xyを求 数学 教えて Goo

对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎

18 7 なのですが 答えのlogyをxで微分す 数学 大学 に関する質問 勉強質問サイト
Http Blog Ncue Edu Tw Sys Lib Read Attach Php Id
Cantor Math Ntnu Edu Tw Wp Content Uploads 09 E6 Ad E5 B9 B4 E5 81 8f E5 Be Ae E5 86 E6 96 B9 E7 A8 8b Pdf

大二高数 函数z Sin X平方y平方 的全微分求函数z X 2
一维波动方程 小时百科
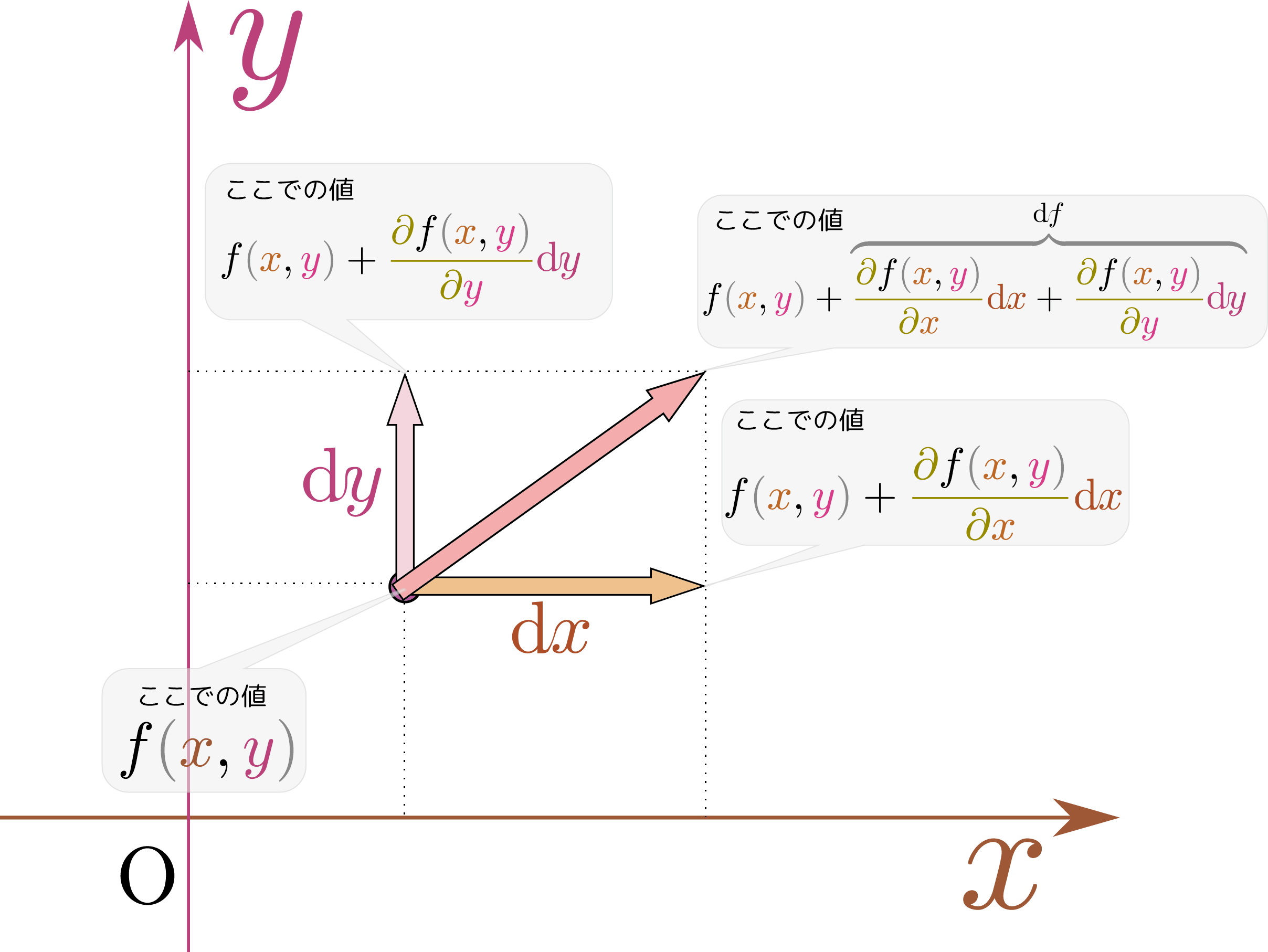
全微分

五点微分 Ln微分 微分公式 微分计算
数学 解決済みの質問 Yahoo 知恵袋

微積分偏微分 考試板 Dcard

对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎

一些偏微分方程的筆記

用python学 微积分b 多元函数的微分 Sagittarius Warrior的博客 Csdn博客 Python多元函数积分
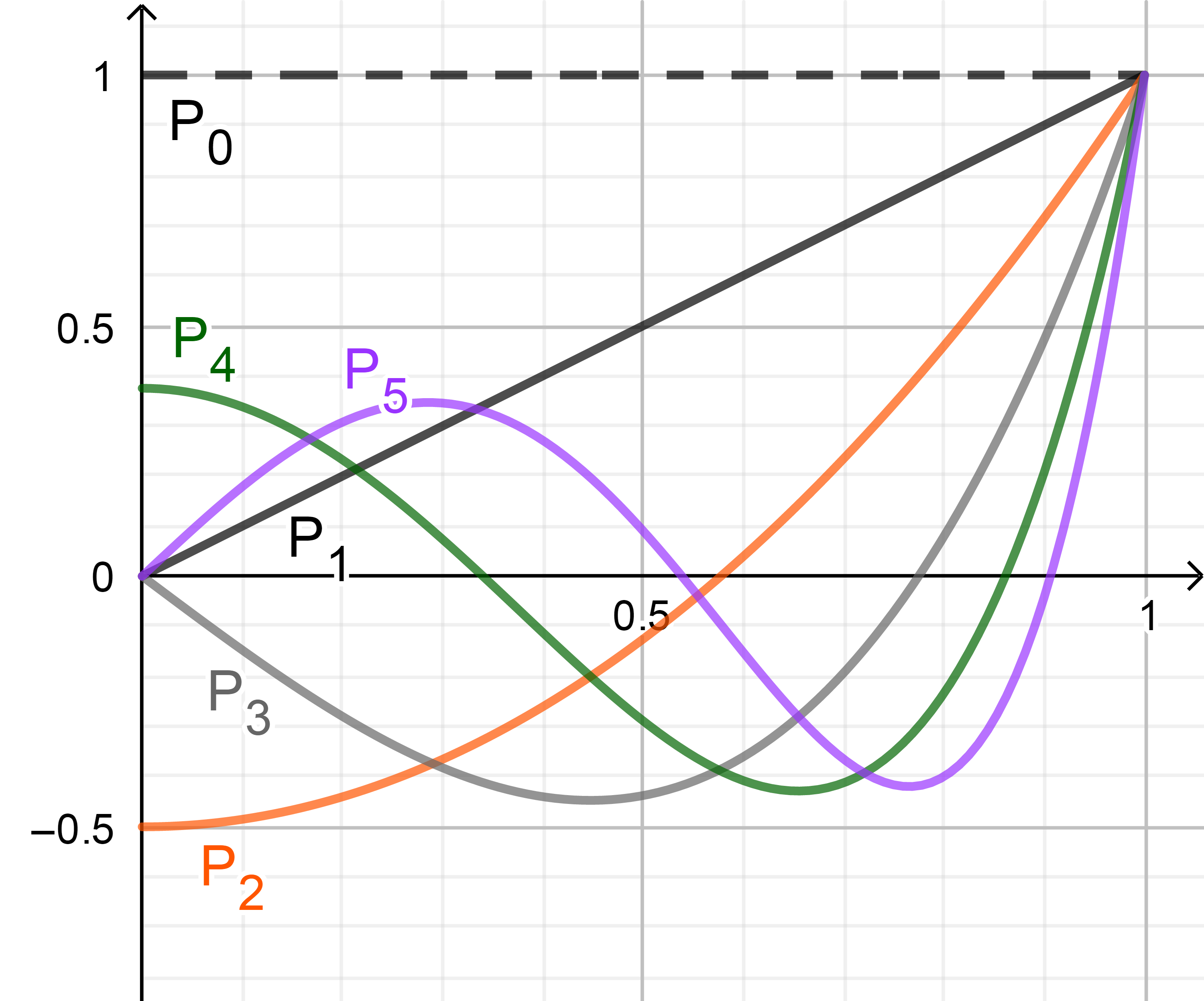
球谐函数 小时百科
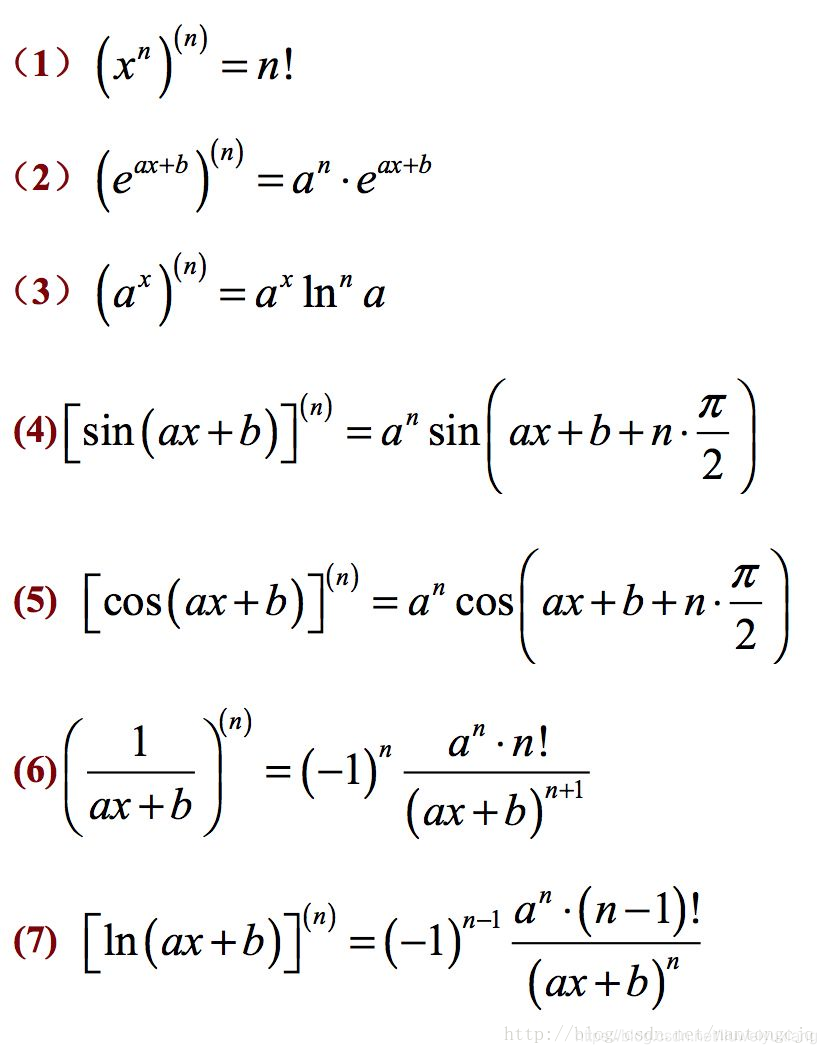
微分和积分公式大全 Lavi的专栏 Csdn博客 积分公式
Gitee Com It Ebooks It Ebooks 1703 Part3 Raw Master E5 81 8f E5 Be Ae E5 86 E6 96 B9 E7 A8 8b E8 Ae B2 E4 B9 Ef E5 A0 E6 8c Af E5 Ae 87 Ef Pdf

数学分析考研试题集锦下载 在线阅读 爱问共享资料
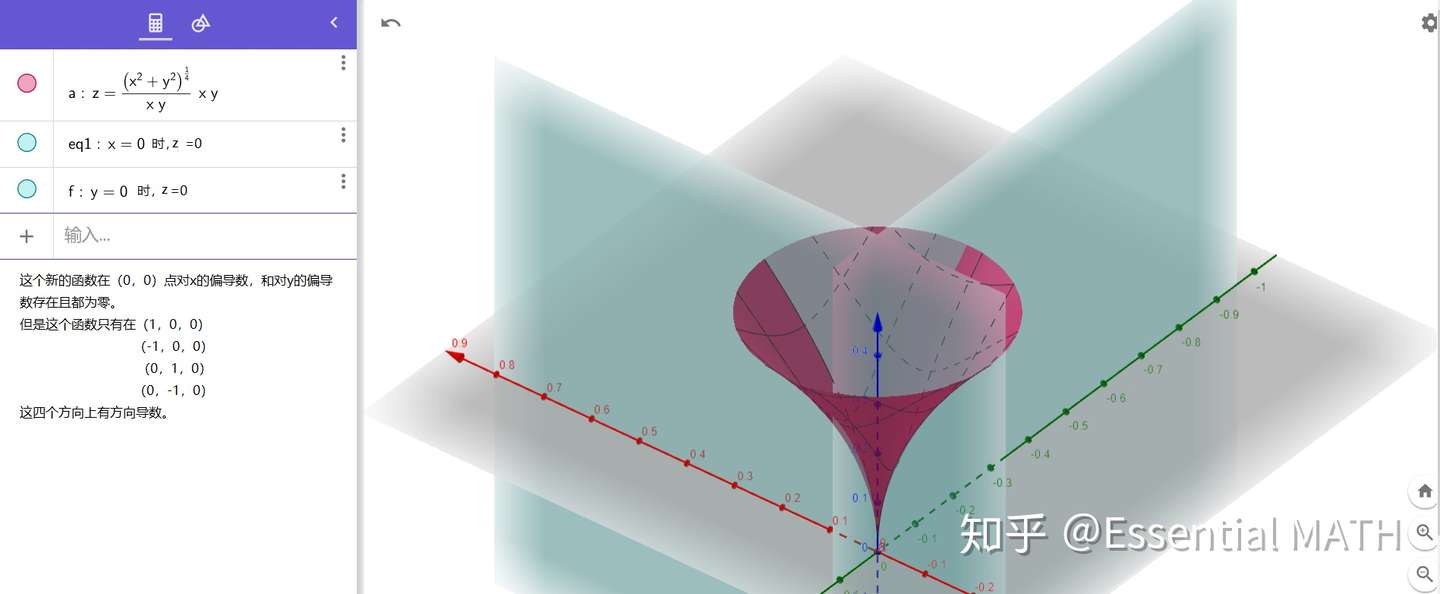
对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎

折纸艺术与偏微分方程 数学与人文

多元函数微分学 程序员大本营

求z Y X 2 Y 2的全微分 雨露学习互助

偏微分のやり方 アークタンジェントxの微分のやり方は知ってい 高校数学に関する質問 勉強質問サイト

Mathematica教程下载 Ppt模板 爱问共享资料

对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎
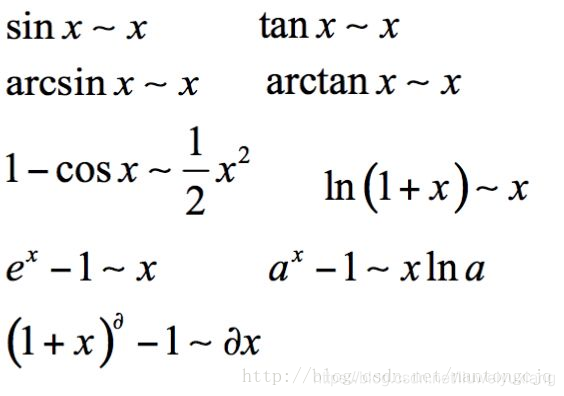
微分和积分公式大全 Lavi的专栏 Csdn博客 积分公式

高等数学多元微积分总结 Jason S Blog

偏微分の変形 数学 大学 に関する質問 勉強質問サイト
复合函数求导链式法则 小时百科

对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎

生物信息学第八章数学模型毛理凯 Ppt Download

题是z F Xy X 2 Y 2 求对x的二阶偏导 不明白为什么一阶偏导仍是u V的二元函数 百度知道

偏微分公式大全 积分公式大全 微分公式表 高等数学微分公式

求函数u Ex X2 Y2 Z2 的全微分 作业 慧海网
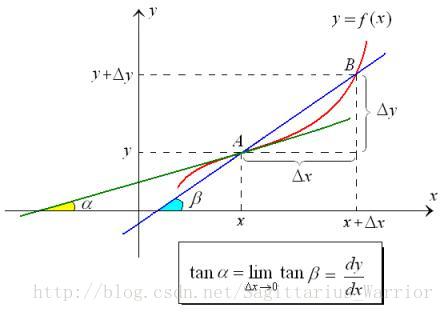
用python学 微积分b 多元函数的微分 Sagittarius Warrior的博客 Csdn博客 Python多元函数积分

期中考试答案

Pde 的深入研究

Chapter8 Partial Derivatives 第八章偏導數 By Etl Tttle Issuu

偏微分公式大全 积分公式大全 微分公式表 高等数学微分公式

偏微分公式大全 积分公式大全 微分公式表 高等数学微分公式

对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎

对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎

对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎

Pdf 泰山学院微分方程教案 Longxiang Li Academia Edu

五点微分 Ln微分 微分公式 微分计算

高等数学多元微积分总结 Jason S Blog
Http Web Math Sinica Edu Tw Math Media D243 Pdf

高等数学多元微积分总结 Jason S Blog

求一阶偏导数w X Y Y Z 作业 慧海网

偏微分 問3で問2と同じことを考えよとのことですが 同じ事とはどう 数学 教えて Goo
Cantor Math Ntnu Edu Tw Wp Content Uploads 09 E6 Ad E5 B9 B4 E5 81 8f E5 Be Ae E5 86 E6 96 B9 E7 A8 8b Pdf

Chapter 11 偏微分方程 Some Notes On Mathematics

对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎

高等数学微分学部分的几道试题一 选择题 每小题3分 1 函数在处 A 不连续 B 连续但偏导数不存在 雨露学习互助
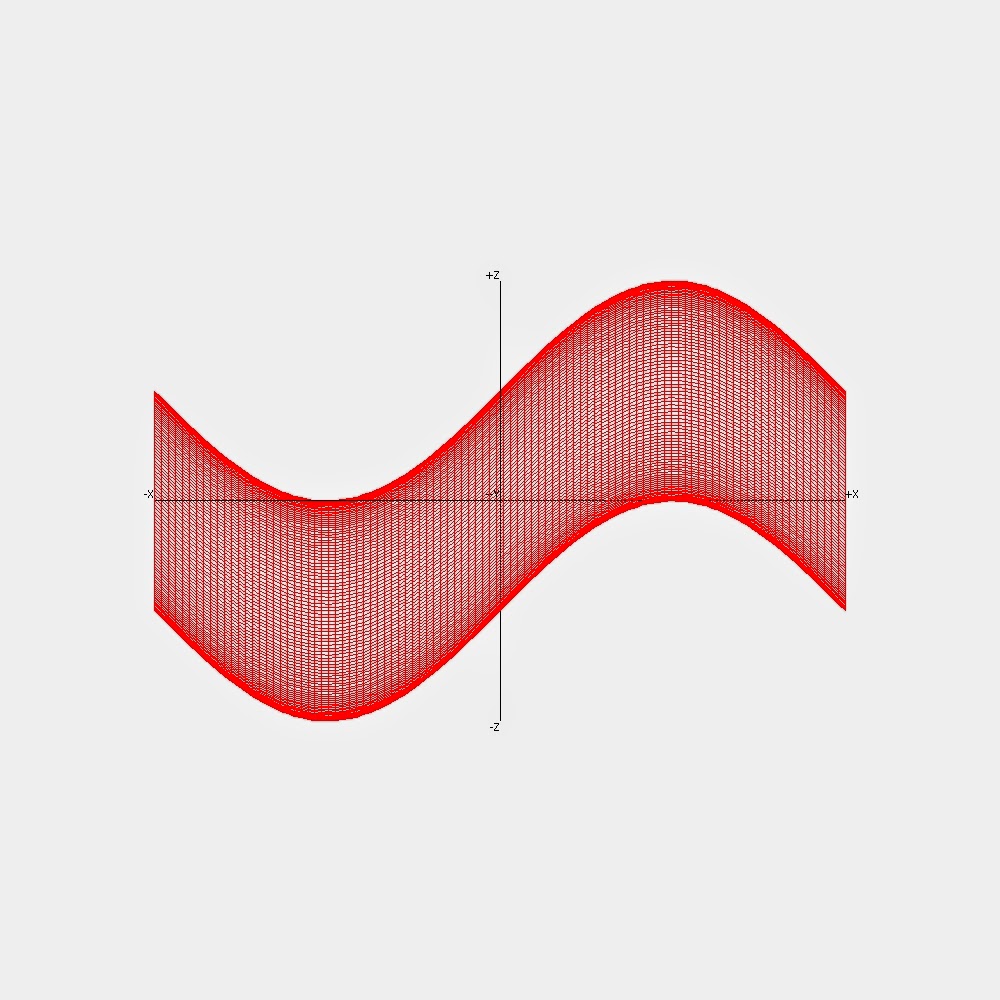
Cosine裡面可以放 1 向量分析大典 偏導數partial Derivative

高等数学多元微积分总结 Jason S Blog
2

15latex学习系列之 Latex里插入数学公式 梦并不遥远 博客园

18 7 なのですが 答えのlogyをxで微分す 数学 大学 に関する質問 勉強質問サイト
Midterm 康宁
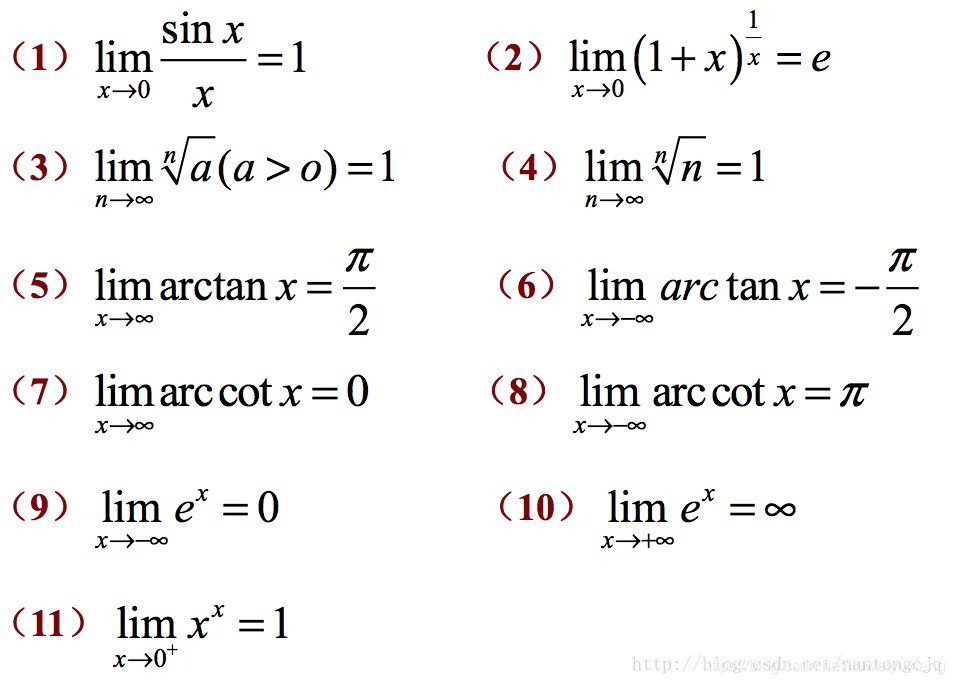
微分和积分公式大全 Lavi的专栏 Csdn博客 积分公式

对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎
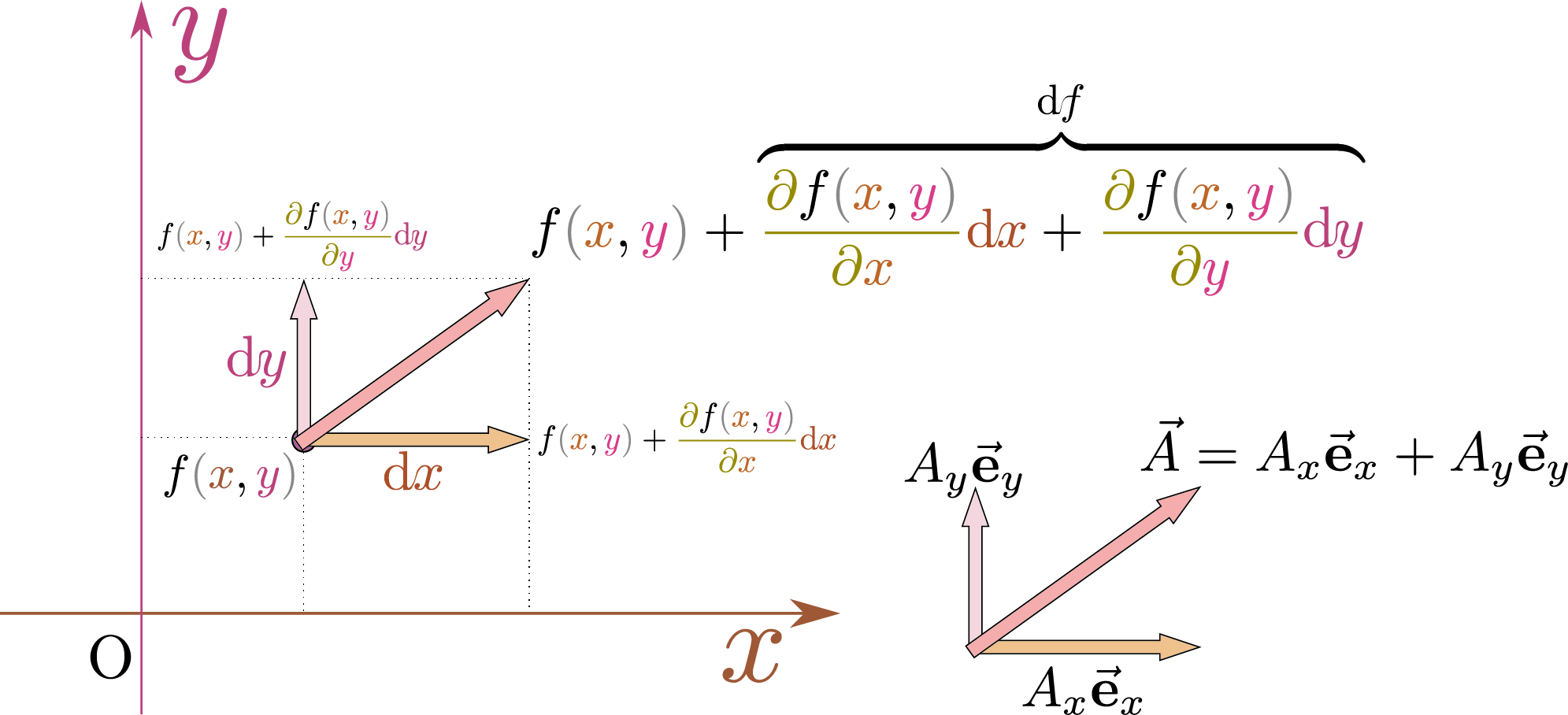
偏微分の注意 続き
Midterm 康宁

求z Y X平方 Y平方的全微分 Z等于y比根下x的平
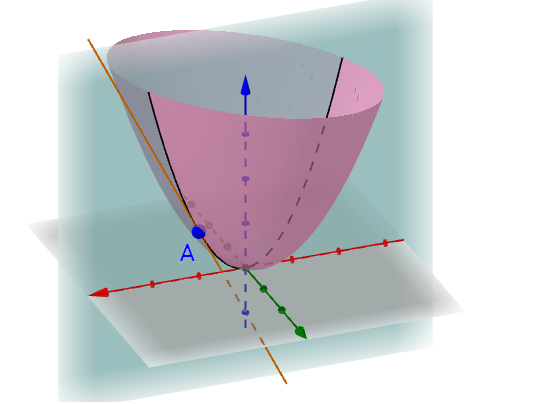
全微分偏微分偏导数
偏微分方程 Partial Differential Equation Ii Wilenwu Csdn博客
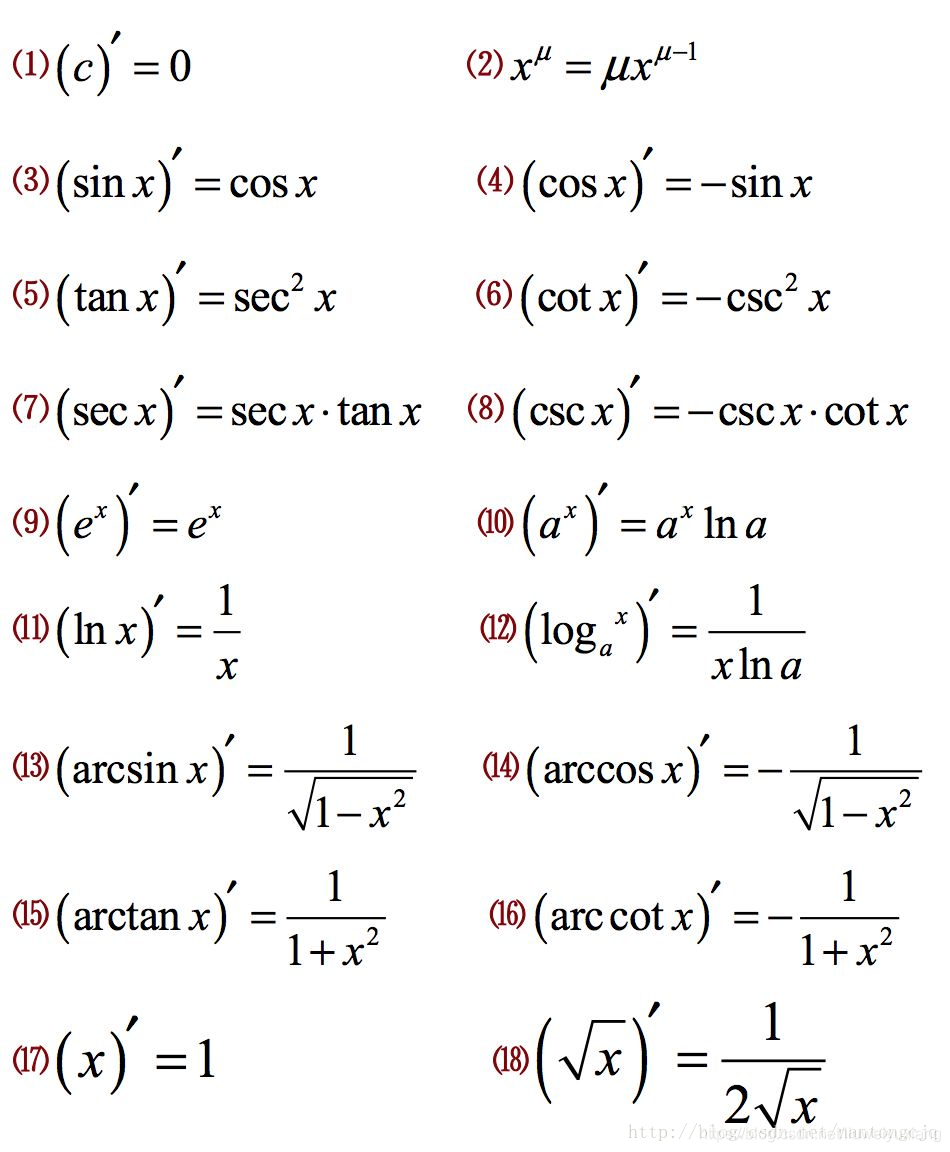
微分和积分公式大全 Lavi的专栏 Csdn博客 积分公式
偏导数 知乎

数学基础系列 二 偏导数 方向导数 梯度 微积分 旧市拾荒 博客园

Chapter 11 偏微分方程 Some Notes On Mathematics
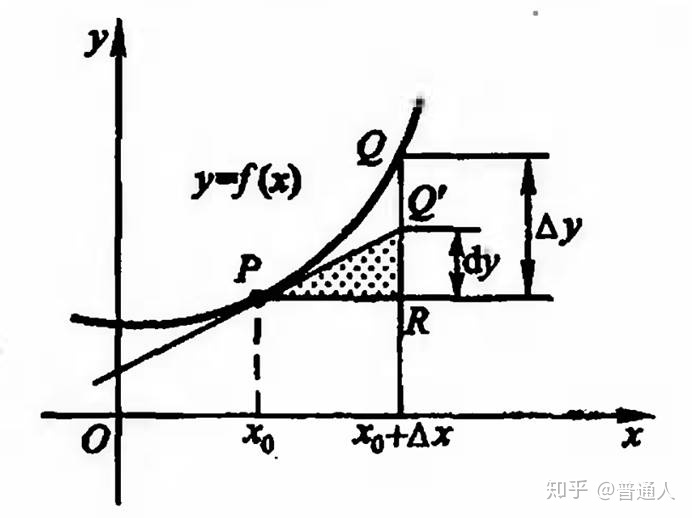
导数 微分 偏导数 偏微分 全微分 Wghou09 博客园
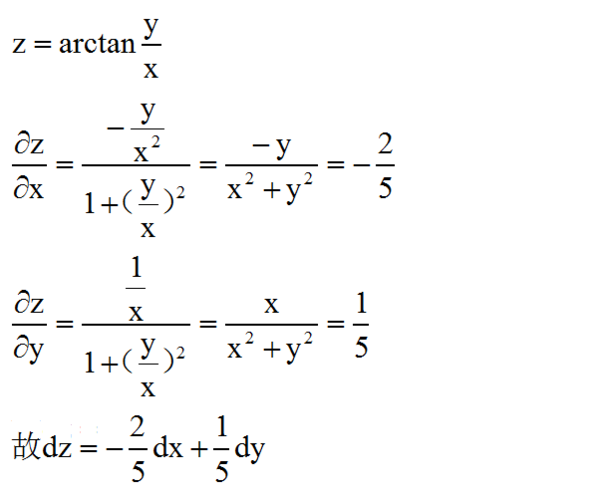
设函数z Arctan Y X 求在点p 1 2 的全微分 360问答

高等数学微分学部分的几道试题一 选择题 每小题3分 1 函数在处 A 不连续 B 连续但偏导数不存在 雨露学习互助

偏微分公式大全 积分公式大全 微分公式表 高等数学微分公式

自主ゼミ 6回目

偏微分の意味とやり方

2 8 二階偏微分と全微分
全微分与函数的近似值 四都教育
偏微分公式大全 积分公式大全 微分公式表 高等数学微分公式
Http Blog Ncue Edu Tw Sys Lib Read Attach Php Id

偏微分公式大全 积分公式大全 微分公式表 高等数学微分公式

Chapter 11 偏微分方程 Some Notes On Mathematics

考研数学公式定理汇总12完全版下载 在线阅读 爱问共享资料

数学建模入门 Matlab实现偏微分方程数值解 Jiajunbernoulli的博客 Csdn博客 Matlab解偏微分方程
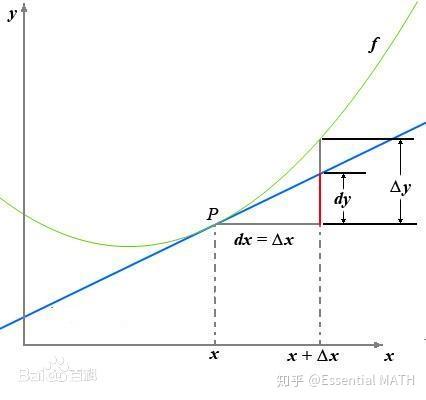
对二元函数的粗糙理解 连续 可微 可偏导 偏微分 各方向导数存在 偏导连续 连续可偏导 知乎

折纸艺术与偏微分方程 数学与人文
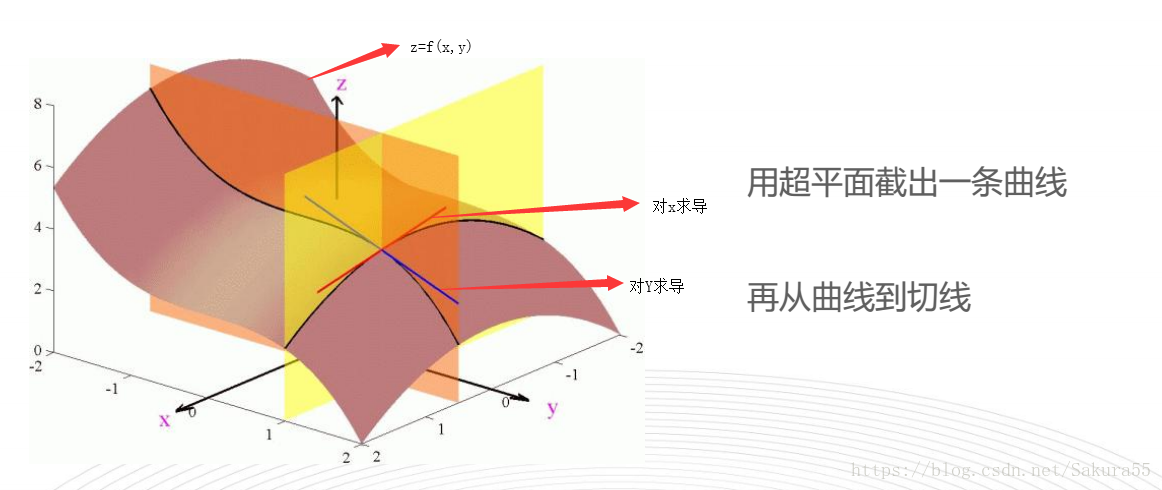
数学必知必会 导数 梯度与积分 樱花落瓣 Csdn博客
Midterm 康宁

問題 雙變數求極值 看板seniorhigh Ptt網頁版
偏微分教えてください Z Y Xのx微分とy微分を求めたいです 途中計算も Yahoo 知恵袋
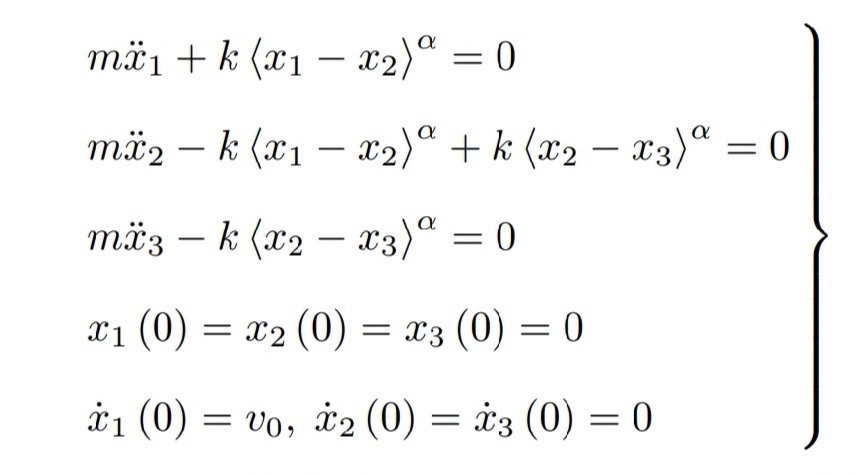
Matlabode45怎样求这个微分方程组数值解啊 Csdn论坛



